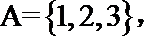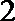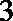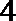- 真题试卷
- 模拟试卷
- 预测试卷
3.如果随机变量 


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合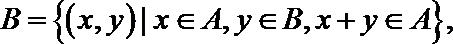
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.执行如图中的程序框图,若输出的结果为21,则判断框中应填( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 如图,在三棱锥










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若平面向量

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 点P是双曲线






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若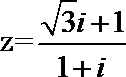

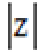
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知实数





正确答案
-3
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知双曲线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知某几何体的三视图如图所示,则该几何体的体积是__________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知角







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知定义在




①
②

③函数

④若关于




以上命题中所有正确的命题的序号为__________。
正确答案
①②④
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在平面直角坐标系


(1)求椭圆
(2)若点










(ⅰ)设直线




(ⅱ)设过点


求证:直线
正确答案
(1)由题意得


消去

解得

所以椭圆

(2)(ⅰ)设



因为


因为


(ⅱ)直线


则直线



所以直线

解析
解析已在路上飞奔,马上就到!
知识点
18.在某次三星杯围棋决赛中,小将A以2:0战胜上届冠军B,引起B所在国围棋界一片哗然!已知三星杯决赛采用的是三局两胜制,若选手A在一次对决中战胜选手B的概率为
(Ⅰ)求选手A战胜选手B的概率;
(Ⅱ)若赛制改为七局四胜制,即选手A战胜选手B所需局数为X,求X的期望.
正确答案
解:(Ⅰ)依题意,选手A战胜选手B分两种情况:2:0和2:1
所以所求概率为0.42+
(Ⅱ)依题意,X可取4,5,6,7,此时选手A战胜选手B的比分为4:0,4:1,4:2,4:3
它们的概率分别为:
P(X=4)=0.44;
P(X=5)=
P(X=6)=
P(X=7)=
故X的期望为4×0.44+5


解析
解析已在路上飞奔,马上就到!
知识点
16.在△
(1)求角
(2) 求
正确答案
(1)因为
由正弦定理,得
所以

因为

(2) 由


因为

当



解析
解析已在路上飞奔,马上就到!
知识点
17.如图,斜三棱柱




(Ⅰ)证明:


(Ⅱ)在平面


正确答案
解:(Ⅰ)面





所以

取






















(Ⅱ)在






在













且


解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(1)求函数

(2)求函数
(3)若存在


正确答案
(1)因为函数
所以

又因为



(2)由(1),
因为当


又


故函数

(3)因为存在

而当

所以只要
又因为


所以


所以当






因为
令

所以

而



当


所以,当


函数


当


函数


综上可知,所求

解析
解析已在路上飞奔,马上就到!
知识点
21. 设


命题

命题




(1)若


(2)对于(1)中的



(3)若





正确答案
解:(1)设



即

(2)当


即“若
对于任意的

当



由①-②得,

当




当


所以


(3)由


设



所以
所以
解析
解析已在路上飞奔,马上就到!