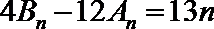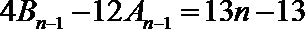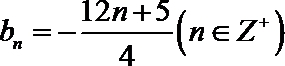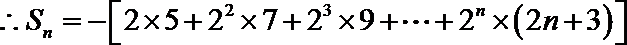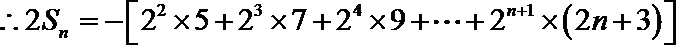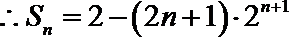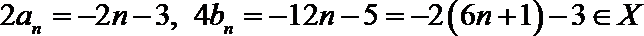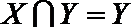- 真题试卷
- 模拟试卷
- 预测试卷
19.在


(1)求
(2)若

正确答案
(1)
又
而
所以
(2)由(1)可知
所以
解析
解析已在路上飞奔,马上就到!
知识点
22.若
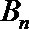
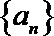
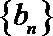
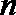
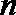
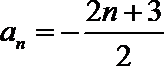
(1)求数列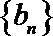
(2)设数列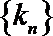
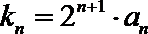
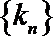
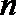
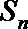
(3)设集合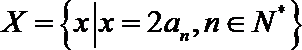
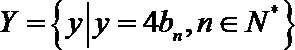
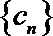
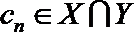
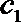


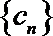
正确答案
(1)∵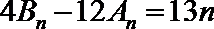
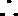
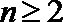
作差得: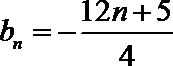
又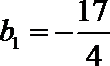
(2)
(3)对任意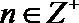
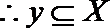
∵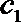
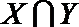
∴
设等差数列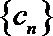
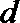
则
∵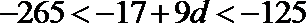
得
而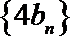
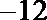
∴
∴
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,圆锥的顶点是






(1)计算圆锥的侧面积;
(2)求

正确答案
(1)
所以,
(2)


解析
解析已在路上飞奔,马上就到!
知识点
21.已知定义域为

(1)求实数
(2)若对于任意的


正确答案
(1)


又
(2)



即
由(1)知


所以
即对一切


解析
解析已在路上飞奔,马上就到!
知识点
23.给定椭圆






(1)求椭圆
(2)点






①当


②求证:
正确答案
(1)
所以,椭圆方程:
准圆方程:
(2)①易知
设直线为
联立
因为椭圆与直线有且只有一个交点,
所以
所以
②<ⅰ>当

设直线
由
同理,联立

由(*)(**)可知,


因此
<ⅱ>当

所以
解析
解析已在路上飞奔,马上就到!
知识点
18.设函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.空间三点
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.下列程序框图中,如果输入三个实数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.“

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知函数



正确答案
9
解析
解析已在路上飞奔,马上就到!
知识点
10.设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知

正确答案
2046
解析
解析已在路上飞奔,马上就到!
知识点
13.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知向量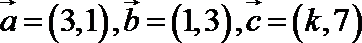
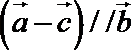
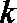
正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
8.已知椭圆
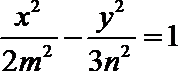
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若函数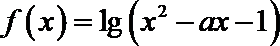
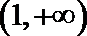
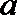
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.一支田径队有男运动员48人,女运动员36人,若用分层抽样的方法从该队的全体运动员中抽取一个容量为21的样本,则抽取男运动员的人数为( )
正确答案
12
解析
解析已在路上飞奔,马上就到!
知识点
7.如图,已知边长为6的正方形







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.将边长为1正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,记

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.将杨晖三角形中的每一个数


观察莱布尼兹三角形规律,计算极限
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.抛物线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设集合
则
正确答案
[0,1)
解析
解析已在路上飞奔,马上就到!
知识点
1.若

正确答案
-4
解析
解析已在路上飞奔,马上就到!