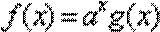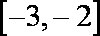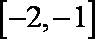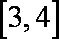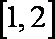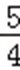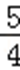- 真题试卷
- 模拟试卷
- 预测试卷
9.已知实数x,y满足约束条件

正确答案
解析
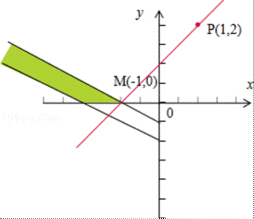
由题意得:作出目标函数2x+y=6,和2x+y=1,
则对应的平面区域如图:则B,C在直线ax+by+c=0上,
由

由

则B,C在直线在直线ax+by+c=0上,∴BC的方程为3x﹣y﹣4=0,
即a=3,b=﹣1,c=﹣4,则
知识点
6.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
正确答案
解析
如图所示,原几何体为:
一个长宽高分别为6,3,6的长方体砍去一个三棱锥,底面为直角边分别为3,4直角三角形,高为4.因此该几何体的体积=3×6×6﹣
知识点
7.执行右图程序框图,如果输入的

正确答案
解析
若x=t=2,
则第一次循环,1≤2成立,则M= 
第二次循环,2≤2成立,则M= 
此时3≤2不成立,输出S=7,
故选:D.
知识点
8.已知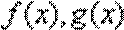
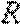
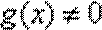
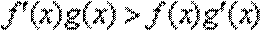
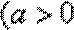

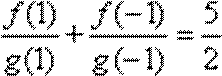
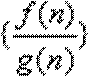
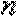
正确答案
解析
∵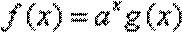
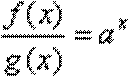
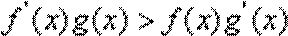
∴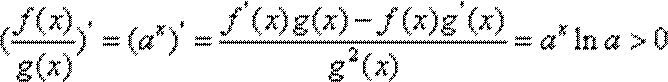
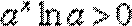
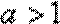
∵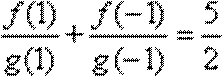
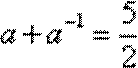
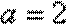
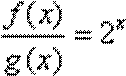
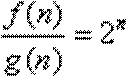
∴数列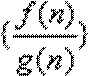
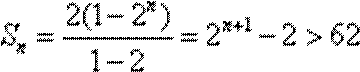
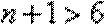
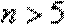
所以
知识点
10.已知抛物线C1:y=

正确答案
解析
由抛物线C1:y=
所以抛物线的焦点坐标为F(0,
由

则抛物线的焦点与双曲线的右焦点的连线所在直线方程为
即
设该直线交抛物线于M(

由题意可知




把M点代入①得:

知识点
1.若全集U=R,集合A={x|x2+x﹣2≤0},B={y|y=log2(x+3),x∈A},则集合A∩(∁UB)=( )
正确答案
解析
A={x|x2+x﹣2≤0}={x|﹣2≤x≤1},
∵B={y|y=log2(x+3),x∈A},由于函数y=log2(x+3)为增函数,
∴B={y|0≤y≤2},
∵全集U=R∴∁UB={y|y<0或y≥2},∴A∩∁UB={x|﹣2≤x<0}.故选:A.
知识点
2.设


正确答案
解析
依题意





知识点
4.设f(x)是定义在R上的奇函数,其f(x)=f(x-2),若f(x)在区间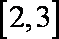
正确答案
解析
由f(x)=f(x﹣2),则函数的周期是2,
若f(x)在区间[2,3]单调递减,则f(x)在区间[0,1]上单调递减,
∵f(x)是定义在R上的奇函数,
∴f(x)在区间[﹣1,0]上单调递减,且f(x)在区间[1,2]上单调递减,
故选:D
知识点
5.将甲、乙、丙等六人分配到高中三个年级,每个年级2人,要求甲必须在高一年级,乙和丙均不能在高三年级,则不同的安排种数为 ( )
正确答案
解析
可以先排高三年级有

知识点
11.已知正三棱柱ABC-A1B1C1的侧棱长与底面边长相等,则AB1与侧面ACC1A1所成角的正弦值等于( )
正确答案
解析
如图,以A1C1中点E为原点建立空间直角坐标系E-xyz,设棱长为1,则A

则sinθ=|cos〈



知识点
12.定义在R上的可导函数f(x)=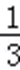
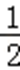
正确答案
解析
∵f(x)=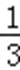
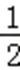
∴f′(x)=x2+ax+2b,
∵函数f(x)在区间(0,1)内取得极大值,在区间(1,2)内取得极小值,
∴f′(x)=x2+ax+2b=0在(0,1)和(1,2)内各有一个根,
f′(0)>0,f′(1)<0,f′(2)>0,
即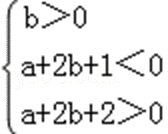
若(1﹣t)a+b+t﹣3>0恒成立,可知a+b﹣3>t(a﹣1)恒成立,由可行域可知a<0,
可得t>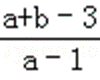
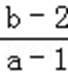
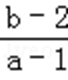
则最小值为1+1=2,
∴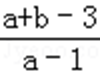
故选:B.
知识点
3.已知向量是单位向量










正确答案
解析
因为











则
即(x,y)到A(1,0)和B(0,2)的距离和为









故选:D.
知识点
13.
正确答案
﹣160
解析


令3﹣r=0,求得r=3,
故展开式中的常数项等于﹣23•
故答案为:-160.
知识点
14.已知函数f(x)=sin(2x+φ)(其中φ为实数),若f(x)≤|f(
正确答案
[kπ+

解析
若f(x)≤|f(
则f(
即2×

则φ=kπ+
又sinφ<0,
令k=﹣1,此时φ=﹣
令2x﹣


解得x∈[kπ+

则f(x)的单调递增区间是[kπ+

故答案为:[kπ+

知识点
15.甲、乙、丙、丁四人商量去看电影。
甲说:乙去我才去;
乙说:丙去我才去;
丙说:甲不去我就不去;
丁说:乙不去我就不去。
最后有人去看电影,有人没去看电影,去的人是
正确答案
甲乙丙
解析
由题意,丙去,则甲乙去,丁不去,即可得出结论。
知识点
16.已知函数










正确答案
2
解析
由已知得M(0,2a),N(a,0),因为





知识点
17.已知数列{an}前n项和为Sn,满足2Sn+ n2 = 3an-6,(n∈N*)
(1)求数列{an}的通项公式;
(2)求证:
(3)设 
正确答案
见解析。
解析
(1)由

当

①-②得


∴

又


(2)由(1)可知

易知




(3)


令

所以


令
即
∴

故
知识点
21.已知在平面直角坐标系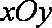
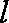

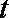

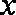
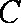
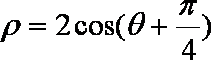
(1)判断直线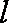
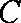
(2)设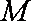
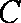
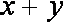
正确答案
见解析。
解析
(1)直线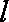
曲线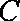
圆心
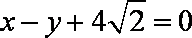
所以直线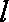
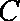
(2)设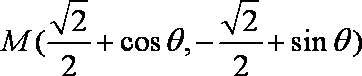
则
知识点
20.如图,已知⊙O1与⊙O2相交于A、B两点,过点A作⊙O1的切线交⊙O2于点C,过点B和两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P。
(1)求证:AD∥EC;
(2)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长。
正确答案
见解析。
解析
(1)∵AC是
又∵∠BAC=∠E,∴∠D=∠E,∴AD∥EC.
(2)设BP=x,PE=y,∵PA=6,PC=2,
∴xy=12 ①
∴DE=9+x+y=16,
∵AD是⊙O2的切线,∴AD2=DB·DE=9×16,
∴AD=12.
知识点
18.直三棱柱


(1)若

(2)当

正确答案
见解析。
解析
(1)证明:当D是AB的中点时, AC1∥平面B1CD.
连接 BC1交B1C与E
连接DE。又DE是三角形ABC1的中位线
所以DE //AC1
所以AC1∥平面B1CD
(2) 由
以C为原点建立如图所示的空间直角坐标系C-xyz.
则B(6, 0, 0),A (0, 8, 0),A1(0, 8,8),B1(6, 0, 8).
设D(a, b, 0)(

因为 点D在线段AB上,且

所以
所以

平面BCD的法向量为
设平面B1CD的法向量为
由 


所以

设二面角


所以二面角

知识点
19.已知椭圆C:

(1)求椭圆的方程;
(2)设







正确答案
见解析。
解析
(1)由题意:以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆的方程为
∴圆心到直线
∵椭圆

故所求椭圆方程为
(2)由题意知直线


将直线方程代入椭圆方程得:
∴
∴
设

当t=0时,直线l的方程为y=0,此时t=0,
当
得
∴
将上式代入椭圆方程得:
整理得:
由
综上所以t∈(-2,2)
知识点
22.已知函数 f(x)=x2+4|x﹣a|(x∈R).
(1)存在实数x1、x2∈[﹣1,1],使得f(x1)=f(x2)成立,求实数a的取值范围;
(2)对任意的x1、x2∈[﹣1,1],都有|f(x1)﹣f(x2)|≤k成立,求实数k的最小值。
正确答案
见解析。
解析
(1)函数 f(x)=x2+4|x﹣a|=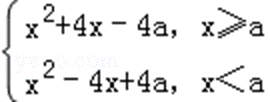
当a≥1时,函数f(x)在[﹣1,1]上单调递减,不满足条件.
当a≤时,函数f(x)在[﹣1,1]上单调递增,不满足条件.
∴﹣1<a<1,此时,函数f(x)在[﹣1,a]上单调递减,在(a,1]上单调递增,
(2)∵对任意的x1、x2∈[﹣1,1],都有|f(x1)﹣f(x2)|≤k成立,
设函数f(x)在[﹣1,1]上的最大值为M(a),最小值为m(a),
当a≥1时,函数f(x)在[﹣1,1]上单调递减,M(a)=f(﹣1)=4a+5,m(a)=f(1)=4a﹣3.
当a≤时,函数f(x)在[﹣1,1]上单调递增,M(a)=f(1)=5﹣4a,m(a)=f(﹣1)=﹣4a﹣3.
∴﹣1<a<1,函数f(x)在[﹣1,a]上单调递减,在(a,1]上单调递增,m(a)=f(a)=a2,M(a)=max{f(1),f(﹣1)}={5﹣4a,5+4a}.
即当0<a<1时,M(a)=5+4a,当﹣1<a<0时,M(a)=5﹣4a.
综上可得,M(a)﹣m(a)=
可得k≥M(a)﹣m(a),
故当a≥1 或a≤﹣1时,k≥8;
当0≤a<1时,k≥﹣a2+4a+5=9﹣(a﹣2)2,由9﹣(a﹣2)2∈[5,8),可得k≥8;
当﹣1<a≤0时,k≥﹣a2﹣4a+5=9﹣(a+2)2,由9﹣(a+2)2∈[5,8),可得k≥8.
综合可得,k≥8。