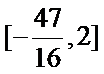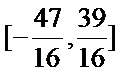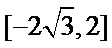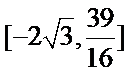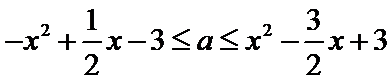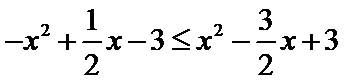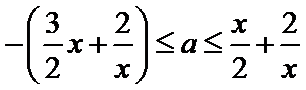- 真题试卷
- 模拟试卷
- 预测试卷
2.设变量


正确答案
解析
目标函数为四边形ABCD及其内部,其中

考查方向
解题思路
画出约束条件的可行域,利用目标函数的最优解求解即可.
易错点
解线性规划问题的基本方法是图解法。当B>0时,动直线





3.阅读右面的程序框图,运行相应的程序,若输入

正确答案
解析
依次为


考查方向
解题思路
根据程序框图,进行模拟计算即可.
易错点
对循环结构中控制条件理解存在偏差
4.设


正确答案
解析



所以是充分不必要条件,选A.
考查方向
解题思路
运用绝对值不等式的解法和正弦函数的图象和性质,化简两已知不等式,结合充分必要条件的定义,即可得到结论.
易错点
解题时最容易出错的就是颠倒了充分性与必要性,所以在解决这类问题时一定要根据充要条件的概念作出准确的判断。
5.已知双曲线




正确答案
解析
由题意得
考查方向
解题思路
由双曲线的离心率为
易错点
注意双曲线中a,b,c之间的关系
1.设集合

正确答案
解析

考查方向
解题思路
由并集概念求得A∪B,再由交集概念得答案.
易错点
对集合表示法部分学生只从形式上“掌握”,对其本质的理解存在误区,常见的错误是不理解集合的表示法,忽视集合的代表元素。
6.已知奇函数




正确答案
解析
奇函数f(x)在R上是增函数,当x>0,f(x)>f(0)=0,且f′(x)>0,
∴g(x)=xf(x),则g′(x)=f(x)+xf′(x)>0,
∴g(x)在(0,+∞)单调递增,且g(x)=xf(x)偶函数,
∴a=g(-log25.1)=g(log25.1),
则2<-log25.1<3,1<20.8<2,
由g(x)在(0,+∞)单调递增,则g(20.8)<g(log25.1)<g(3),
∴b<a<c,
故选C.
考查方向
解题思路
由奇函数f(x)在R上是增函数,则g(x)=xf(x)偶函数,且在(0,+∞)单调递增,则a=g(-log25.1)=g(log25.1),则2<-log25.1<3,1<20.8<2,即可求得b<a<c
易错点
无
7.设函数







正确答案
解析
由题意








考查方向
解题思路
由题意求得



易错点

8.已知函数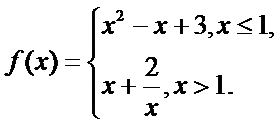
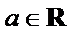
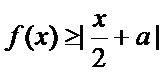
正确答案
解析
当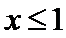
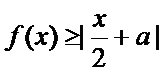
即为
即有
由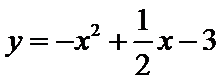
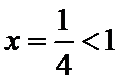
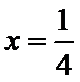
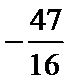
由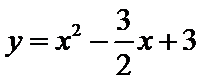
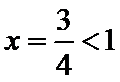
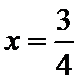
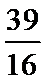
则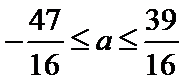
当x>1时,关于x的不等式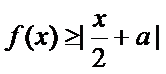
即为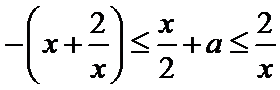
即有
由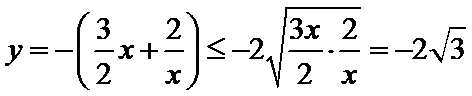
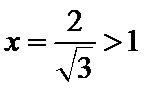
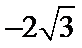
由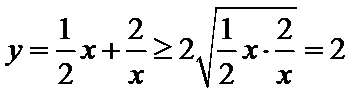
则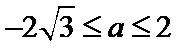
由①②可得,-
综上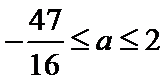
考查方向
解题思路
讨论当x≤1时,运用绝对值不等式的解法和分离参数,可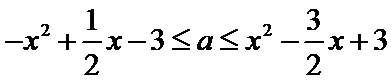
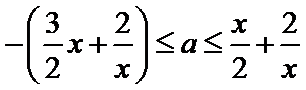
易错点
与分段函数相关的问题有作图、求值、求值域、解方程、解不等式、研究单调性及讨论奇偶性等等。在解决此类问题时,要注意分段函数是一个函数而不是几个函数,如果自变量取值不能确定,要对自变量取值进行分类讨论,同时还要关注分界点附近函数值变化情况。
9.已知

正确答案
解析

则
考查方向
解题思路
运用复数的除法法则,结合共轭复数,化简
易错点
要善于掌握化虚为实的转化方法,即设复数z=a+bi(a,b∈R),但有时给许多问题的求解带来不必要的运算困难,而若把握复数的整体性质运用整体运算的思想方法,则能事半功倍,同时要注意复数几何意义的应用
10.已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为 .
正确答案
解析
设正方体边长为

外接球直径为
考查方向
解题思路
根据正方体和球的关系,得到正方体的体对角线等于直径,结合球的体积公式进行计算即可.
易错点
熟记球的体积公式.
11.在极坐标系中,直线

正确答案
2
解析
直线为


考查方向
解题思路
把极坐标方程化为直角坐标方程,求出圆心到直线的距离d,与半径比较即可得出位置关系.
易错点
极坐标方程与直角坐标方程的互化.
13.在







正确答案
解析

则
考查方向
解题思路
根据题意画出图形,结合图形,利用
表示出

易错点
无
14.用数字1,2,3,4,5,6,7,8,9组成没有重复数字,且至多有一个数字是偶数的四位数,这样的四位数一共有___________个.(用数字作答)
正确答案
解析
根据题意,分2种情况讨论:
①四位数中没有一个偶数数字,即在1、3、5、7、9种任选4个,组成一共四位数即可,
有A54=120种情况,即有120个没有一个偶数数字四位数;
②四位数中只有一个偶数数字,
在1、3、5、7、9种选出3个,在2、4、6、8中选出1个,有C53•C41=40种取法,
将取出的4个数字全排列,有A44=24种顺序,
则有40×24=960个只有一个偶数数字的四位数;
则至多有一个数字是偶数的四位数有120+960=1080个;
故答案为:1080.
考查方向
解题思路
根据题意,要求四位数中至多有一个数字是偶数,分2种情况讨论:①、四位数中没有一个偶数数字,②、四位数中只有一个偶数数字,分别求出每种情况下四位数的数目,由分类计数原理计算可得答案.
易错点
注意不重不漏.
12.若


正确答案
4
解析


考查方向
解题思路
两次利用基本不等式,即可求出最小值,需要注意不等式等号成立的条件是什么.
易错点
均值不等式


在解题过程中,务必要先检验取等号的三个条件是否成立。常规的解法是①如果积或和不是定值,设法构造“定值”;② 若是
15.在





(Ⅰ)求

(Ⅱ)求
正确答案
(1) 

解析
(Ⅰ)在△ABC中,∵

由已知及余弦定理,有b2=a2+c2−2accosB=25+36−2×5×6×
∴
由正弦定理

∴

(Ⅱ)由(Ⅰ)及



故
考查方向
解题思路
(Ⅰ)由已知结合同角三角函数基本关系式求得cosB,再由余弦定理求得b,利用正弦定理求得sinA;
(Ⅱ)由同角三角函数基本关系式求得cosA,再由倍角公式求得sin2A,cos2A,展开两角和的正弦得答案.
易错点
在解三角形中,要注意挖掘题中的隐含条件,否则范围将扩大或缩小,导致错解
17.如图,在三棱锥P-ABC中,PA⊥底面ABC,
(Ⅰ)求证:MN∥平面BDE;
(Ⅱ)求二面角C-EM-N的正弦值;
(Ⅲ)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为
正确答案
(1)证明见解析(2)

解析
(Ⅰ)证明:取AB中点F,连接MF、NF,
∵M为AD中点,∴MF∥BD,
∵BD⊂平面BDE,MF⊄平面BDE,∴MF∥平面BDE.
∵N为BC中点,∴NF∥AC,
又D、E分别为AP、PC的中点,∴DE∥AC,则NF∥DE.
∵DE⊂平面BDE,NF⊄平面BDE,∴NF∥平面BDE.
又MF∩NF=F.
∴平面MFN∥平面BDE,则MN∥平面BDE;
(Ⅱ)解:∵PA⊥底面ABC,∠BAC=90°.
∴以A为原点,分别以AB、AC、AP所在直线为x、y、z轴建立空间直角坐标系.
∵PA=AC=4,AB=2,
∴A(0,0,0),B(2,0,0),C(0,4,0),M(0,0,1),N(1,2,0),E(0,2,2),
则

设平面MEN的一个法向量为
由


由图可得平面CME的一个法向量为
∴cos<

∴二面角C﹣EM﹣N的余弦值为

(Ⅲ)解:设AH=t,则H(0,0,t),

∵直线NH与直线BE所成角的余弦值为
∴|cos<



解得:t=

∴当H与P重合时直线NH与直线BE所成角的余弦值为


考查方向
解题思路
(Ⅰ)取AB中点F,连接MF、NF,由已知可证MF∥平面BDE,NF∥平面BDE.得到平面MFN∥平面BDE,则MN∥平面BDE;
(Ⅱ)由PA⊥底面ABC,∠BAC=90°.可以A为原点,分别以AB、AC、AP所在直线为x、y、z轴建立空间直角坐标系.求出平面MEN与平面CME的一个法向量,由两法向量所成角的余弦值得二面角C-EM-N的余弦值,进一步求得正弦值;(Ⅲ)设AH=t,则H(0,0,t),求出
的坐标,结合直线NH与直线BE所成角的余弦值为
易错点
在解决有关该考点的具体问题时,易出现的问题主要有:(1)对空间线面关系考虑不全面,导致位置关系判断出错,漏掉直线在平面内的情况;(2)在利用空间线面平行与面面平行的性质定理证明空间平行关系时,往往忽略限制条件导致思维过程不严谨,导致误判
20.设





(Ⅰ)求
(Ⅱ)设


(Ⅲ)求证:存在大于0的常数



正确答案
(1)增区间是


解析
(Ⅰ)由

进而可得



当x变化时,
所以,



(Ⅱ)证明:由


令函数H1(x)=g(x)(x﹣x0)﹣f(x),则H′1(x)=g′(x)(x﹣x0).
由(Ⅰ)知,当x∈[1,2]时,g′(x)>0,
故当x∈[1,x0)时,H′1(x)<0,H1(x)单调递减;
当x∈(x0,2]时,H′1(x)>0,H1(x)单调递增.
因此,当x∈[1,x0)∪(x0,2]时,H1(x)>H1(x0)=﹣f(x0)=0,可得H1(m)>0即h(m)>0,
令函数H2(x)=g(x0)(x﹣x0)﹣f(x),则H′2(x)=g′(x0)﹣g(x).由(Ⅰ)知,g(x)在[1,2]上单调递增,故当x∈[1,x0)时,H′2(x)>0,H2(x)单调递增;当x∈(x0,2]时,H′2(x)<0,H2(x)单调递减.因此,当x∈[1,x0)∪(x0,2]时,H2(x)>H2(x0)=0,可得得H2(m)<0即h(x0)<0,.
所以,h(m)h(x0)<0.
(Ⅲ)证明:对于任意的正整数 


令

由(II)知,当


当


所以h(x)在(1,2)内至少有一个零点,不妨设为x1,则h(x1)=g(x1)(

由(Ⅰ)知g(x)在[1,2]上单调递增,故0<g(1)<g(x1)<g(2),
于是|



因为当x∈[1,2]时,g(x)>0,故f(x)在[1,2]上单调递增,
所以f(x)在区间[1,2]上除x0外没有其他的零点,而

又因为p,q,a均为整数,所以|2p4+3p3q﹣3p2q2﹣6pq3+aq4|是正整数,
从而|2p4+3p3q﹣3p2q2﹣6pq3+aq4|≥1.
所以


考查方向
解题思路
(Ⅰ)求出函数的导函数
(Ⅱ)由

令函数H1(x)=g(x)(x-x0)-f(x),求出导函数H′1(x)利用(Ⅰ)知,推出h(m)h(x0)<0.
(Ⅲ)对于任意的正整数p,q,且

由(Ⅱ)知,当m∈[1,x0)时,当m∈(x0,2]时,通过h(x)的零点.转化推出|



易错点
对“导数值符号”与“函数单调性”关系理解不透彻
16.从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为
(Ⅰ)设

(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
正确答案
(1)
解析
(Ⅰ)随机变量




所以,随机变量
随机变量

(Ⅱ)设


所以,这2辆车共遇到1个红灯的概率为
考查方向
解题思路
(Ⅰ)随机变量X的所有可能取值为0,1,2,3,求出对应的概率值,
写出它的分布列,计算数学期望值;
(Ⅱ)利用相互独立事件同时发生的概率公式计算所求事件的概率值.
易错点
解答此类题常见的错误为①事件的概率不会求;②所求的事件概率不满足

18.已知





(Ⅰ)求

(Ⅱ)求数列

正确答案
(1)


解析
(I)设等差数列



由已知b2+b3=12,得b1(q+q2)=12,而b1=2,所以q+q2-6=0.
又因为q>0,解得q=2.所以,bn=2n.
由b3=a4-2a1,可得3d-a1=8①.
由S11=11b4,可得a1+5d=16②,
联立①②,解得a1=1,d=3,由此可得an=3n-2.
所以,数列{an}的通项公式为an=3n-2,数列{bn}的通项公式为bn=2n.
(II)设数列{a2nb2n-1}的前n项和为Tn,
由


故

上述两式相减,得
得
所以,数列


考查方向
解题思路
(Ⅰ)设出公差与公比,利用已知条件求出公差与公比,然后求解{an}和{bn}的通项公式;
(Ⅱ)化简数列的通项公式,利用错位相减法求解数列的和即可.
易错点
用错位相减法求和时项数处理不当
19.设椭圆








(I)求椭圆的方程和抛物线的方程;
(II)设













正确答案
(1)



解析
(Ⅰ)解:设








所以,椭圆的方程为

(Ⅱ)解:直线l的方程为x=﹣1,设直线AP的方程为x=my+1(m≠0),
联立方程组


联立方程组

∴B(

∴直线BQ的方程为(



令y=0,解得x=

∴|AD|=1﹣

又∵△APD的面积为



整理得3m2﹣2


所以,直线


考查方向
解题思路
(I)根据椭圆和抛物线的定义、性质列方程组求出a,b,p即可得出方程;
(II)设AP方程为x=my+1,联立方程组得出B,P,Q三点坐标,从而得出直线BQ的方程,解出D点坐标,根据三角形的面积列方程解出m即可得出答案.
易错点
解决直线与圆锥曲线位置关系时,常规的方法是设出直线方程,然后与圆锥曲线方程联立,转化为方程的根与系数间的关系问题求解,因此应注意以下几个问题①所设直线的斜率是否存在,②消元后的方程是否为一元二次方程,③一元二次方程是否有实根