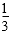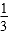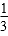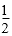- 真题试卷
- 模拟试卷
- 预测试卷
1.设全集
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 若复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设双曲线C:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知约束条件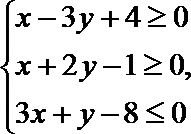
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设p:x2-x-20>0,q:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 设偶函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 设平面向量a=(x1,y1),b=(x2,y2) ,定义运算⊙:a⊙b =x1y2-y1x2 .已知平面向量a,b,c,则下列说法错误的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 执行如图所示的程序框图所表示的程序,则所得的结果为( ).
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 在

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知函数



正确答案
(-1,1)
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知圆的方程为




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 正四面体的






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 前12个正整数组成一个集合


正确答案
369
解析
解析已在路上飞奔,马上就到!
知识点
18.在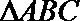
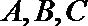
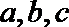

(1)求角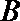
(2)若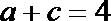
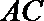
正确答案
(1)由题意得: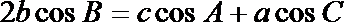
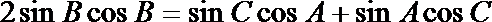

(2)设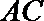
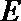
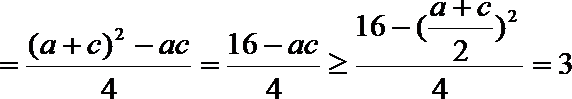
所以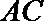
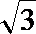
解析
解析已在路上飞奔,马上就到!
知识点
19.设数列






(1)求数列
(2)设





正确答案
(1) 由已知



解得


(2)
因为


注意到,当



所以


对于任意的正整数

所以

即所求实数

解析
解析已在路上飞奔,马上就到!
知识点
21.已知点




(1)求切点
(2)若离心率为







正确答案
(1)设切点

由切线








(2)由(Ⅰ) 得

设





由

将



椭圆方程为
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,已知长方形







(1)求证:
(2)点




正确答案
取AM的中点O,AB的中点B,则




(1)由于


(2)
设存在满足条件的点E,并设
则
则点E的坐标为




则
则








解析
解析已在路上飞奔,马上就到!
知识点
22.函数










(1)若函数


(2)若


正确答案
(1)由于



所以,



(2)由于



而




设对正整数k有

当x=0时,
当

而

当


故

又


所以,
解析
解析已在路上飞奔,马上就到!