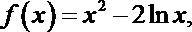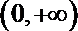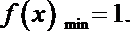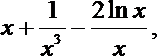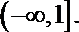- 真题试卷
- 模拟试卷
- 预测试卷
1.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.一个几何体的三视图如图1所示,已知这个几何体的体积为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设


①若a∥

②若a∥



③若a⊥



④若a、b在平面
其中正确命题是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知等比数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.阅读如图所示的程序框图,输出的结果
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设直线kx-y+1=0被圆O: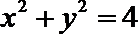
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.直线






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知定义在










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.若不等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
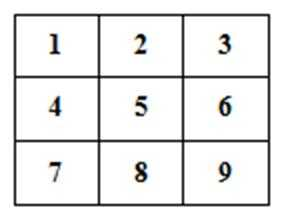
16.用红、黄、蓝三种颜色之一去涂图中标号为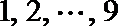
正确答案
108
解析
解析已在路上飞奔,马上就到!
知识点
15.若直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
18.定义在R上的奇函数


(1)求

(2)判断

(3)当


正确答案
解:(1)当
又

当


(2)设


(3)即求函数

当



当


当




解析
解析已在路上飞奔,马上就到!
知识点
17.△ABC的角A、B、C的对边分别为a、b、c,


(Ⅰ)求角A的大小;
(Ⅱ)当

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.
(1)求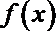
(2)若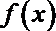
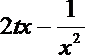
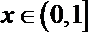
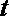
正确答案
解:(1)函数的定义域为
设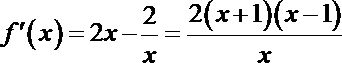

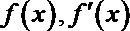
所以,当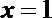
(2)由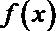
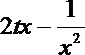
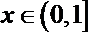
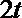
令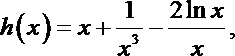
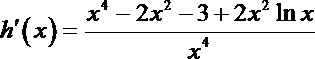
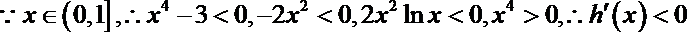
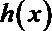
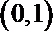
∴当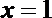
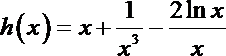
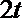
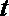
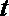
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,已知







(1) 求证:

(2) 求证:平面

(3) 求直线

正确答案
方法一:
(1) 证法一:取


∵



∵



∴

又

∴四边形

∵



∴

证法二:取


∵


∵




又
∴四边形

∵



∴



又


∵

∴

(2) 证:∵



∵




又


∵


∵



(3)解:在平面




∵平面



∴


设


R t△

∴直线


方法二:
设


∵


(1) 证:
∵




(2) 证:∵
∴

∴





(3) 解:设平面




又




∴直线


解析
解析已在路上飞奔,马上就到!
知识点
22.已知圆

(1)求以圆O与y轴的交点为顶点,直线在x轴上的截距为半长轴长的椭圆C方程;
(2)已知点A
正确答案
解:(1) 因为直线
直线的方程变为
所以椭圆方程为
(2)设直线AE方程为
代入
设E


所以
又直线AF的斜率与AE的斜率互为相反数,
同理可得:
所以直线EF的斜率为
解析
解析已在路上飞奔,马上就到!
知识点
21.设





(1)求证:数列
(2)设数列




(3)在满足(2)的条件下,求数列


正确答案
(1)证明:当


当


又


∴ 数列

(2)解:由(1)得,

∵


∴

∴


(3)解:由(2)知

所以
即
则
②-①得
故
解析
解析已在路上飞奔,马上就到!