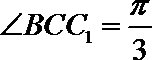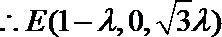- 真题试卷
- 模拟试卷
- 预测试卷
3.命题“∀

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.一几何体的三视图如右图所示,则该几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.由函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.如下图所示的韦恩图中,








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.对任意非零实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若复数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.如下面左图所示,半径为















正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知


正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
16.对于定义在区间










①“平顶型”函数在定义域内有最大值;
②函数

③函数

④当


其中正确的是_______.(填上所有正确结论的序号)
正确答案
①④
解析
解析已在路上飞奔,马上就到!
知识点
14.在直角梯形






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 甲乙两班进行消防安全知识竞赛,每班出3人组成甲乙两支代表队,首轮比赛每人一道必答题,答对则为本队得1分,答错或不答都得0分,已知甲队3人每人答对的概率分别为


(1)求随机变量

(2)求在甲队和乙队得分之和为4的条件下,甲队比乙队得分高的概率。
正确答案
(1)




解析
解析已在路上飞奔,马上就到!
知识点
20.设圆
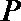
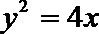
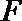
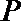
(I)求圆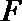
(Ⅱ)过点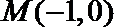
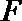
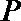
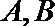
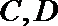
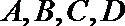
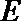
正确答案
(Ⅰ)设圆F的方程为(x-1)2+y2=r2(r>0).
将y2=4x代入圆方程,得(x+1)2=r2,所以x=-1-r(舍去),或x=-1+r.
圆与抛物线有且只有一个公共点,当且仅当-1+r=0,即r=1.
故所求圆F的方程为(x-1)2+y2=1.
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知


(1)求角
(2)试求

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数
(1)求函数
(2)若函数


正确答案

解析
解析已在路上飞奔,马上就到!
知识点
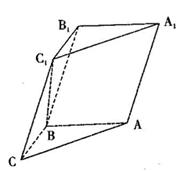
19. 如图,在三棱柱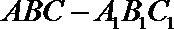
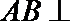
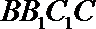
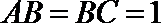
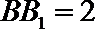
(1)求证: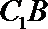
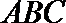
(2)设λ=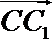
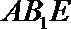
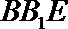
正确答案
(1)因为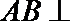
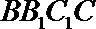
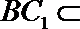
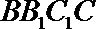
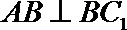
在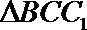
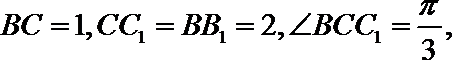
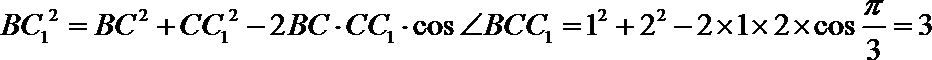
所以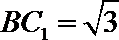
故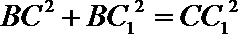
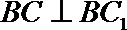
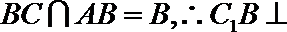
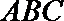
(2)由(1)可知,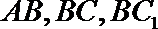
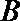
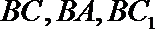
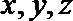
则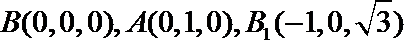
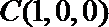
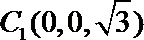
所以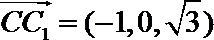
所以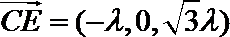
则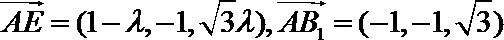
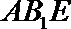
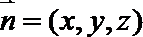
则由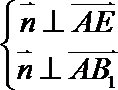
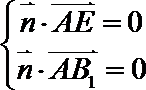
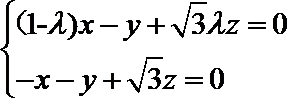
令
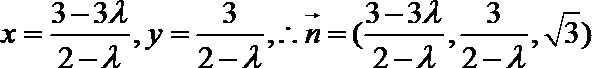
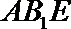
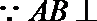
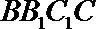
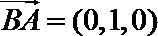

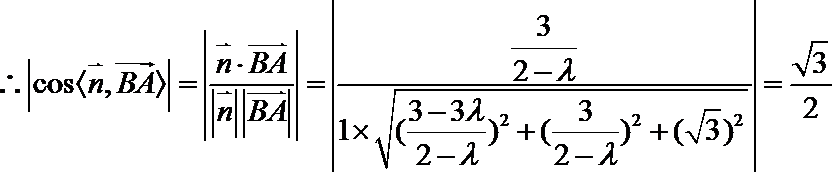
两边平方并化简得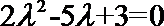
所以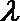
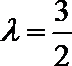
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24三题中任选一题做答。注意:只能做选定的题目。如果多做,则按所做的第一题计分。
22. 选修4—1:几何证明选讲
如图,AB为⊙O的直径,点D是⊙O上的一点,点C是弧
(Ⅰ)证明:
(Ⅱ)若GD=

23. 选修4-4:坐标系与参数方程
在直角坐标系中,以原点为极点,





(I)求曲线

(Ⅱ)若

24. 已知

求证:
正确答案
23.
24.(1)要证明a+b+c≥,
∵a,b,c为正实数,
∴只需证明(a+b+c)2≥3,
即证明a2+b2+c2+2ab+2bc+2ac≥3.
又ab+bc+ac=1,
∴只需证明a2+b2+c2≥ab+bc+ac.
上式可由ab+bc+ca≤++=a2+b2+c2证得,
∴原不等式成立.
(2)略。
解析
解析已在路上飞奔,马上就到!