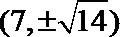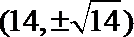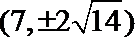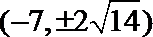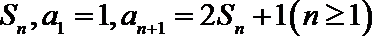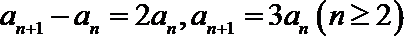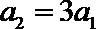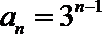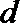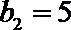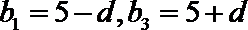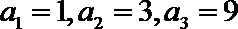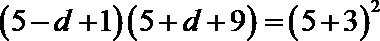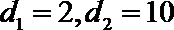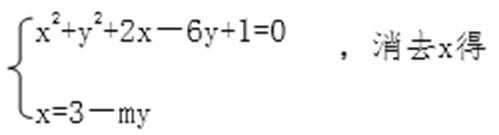- 真题试卷
- 模拟试卷
- 预测试卷
2.已知等差数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知数列-1,a1,a2,-4成等差数列,-1,b1,b2,b3,-4成等比数列,则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.双曲线2x2-y2=8的实轴长是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.如果等差数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设Sn是等差数列{an}的前n项和,若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.以A(1,3)和B(-5,1)为端点的线段AB的垂直平分线方程是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.直线过点P(0,2),且截圆
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知椭圆



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.椭圆

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若抛物线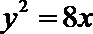
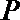
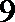
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.等比数列{an}中,a2=9,a5=243,则{an}的前4项和为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在

正确答案
216
解析
解析已在路上飞奔,马上就到!
知识点
16.以下四个关于圆锥曲线的命题中:
①设A、B为两个定点,k为非零常数,
②过定圆C上一定点A作圆的动点弦AB,O为坐标原点,若
③方程
④双曲线

其中真命题的序号为_____________(写出所有真命题的序号)
正确答案
③
解析
解析已在路上飞奔,马上就到!
知识点
13.在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.数列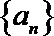
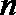
(1)求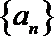
(2)等差数列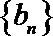
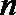
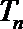
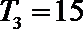
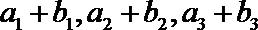
正确答案
(1)由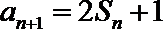
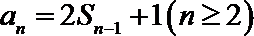
又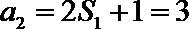
故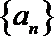
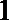

∴
(2)设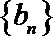
由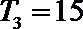
可得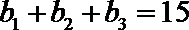
可得
故可设
又
由题意可得
解得
∵等差数列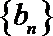
∴
∴
解析
解析已在路上飞奔,马上就到!
知识点
17.已知等差数列




(1)求

(2)令bn=



正确答案
(1)设等差数列
因为

所以有

解得
所以



(2)由(1)知
所以bn=


所以


即数列


解析
解析已在路上飞奔,马上就到!
知识点
20.动圆M过定点A(-

(1)求动圆圆心M的轨迹C的方程;
(2)过点P(0,2)的直线l与轨迹C交于不同的两点E、F,求
正确答案
(1)A´(
依题意有|MA´|+

=2
∴点M的轨迹是以A´、A为焦点,2
∵a=
∴b2=1.
因此点M的轨迹方程为
(2) 解:设l的方程为x=k(y-2)代入
消去x得:(k2+3)y2-4k2y+4k2-3=0
由△>0得
16k4-(4k2-3)(k2+3)>0 
设E(x1,y1),F(x2,y2),
则y1+y2=
又

∴

=k(y1-2)·k (y2-2) +(y1-2)(y2-2)
=(1+k2)
=
∵0≤k2<1
∴3≤k2+3<4
∴

解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆



(1)求椭圆
(2)设O为坐标原点,点A,B分别在椭圆



正确答案
(1)由已知可设椭圆
其离心率为
故
则
故椭圆的方程为
(2)解法一 
由




因此可以设直线
将

得
所以
将

则
所以
由
得
即
解得
故直线

解法二 
由




因此可以设直线
将

得
所以
由
得
将

得
即
解得
故直线


(1)F抛物线C:x2=2py(p>0)的焦点F
设M

由题意可知
则点Q到抛物线C的准线的距离为

解得
于是抛物线C的方程为
(2)假设存在点M,使得直线MQ与抛物线C相切于点M,
而




由
可得

则
即
而
解得

解析
解析已在路上飞奔,马上就到!
知识点
19.已知圆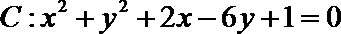
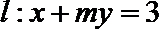
(1)若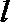
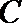
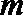
(2)是否存在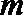
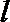
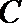
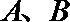
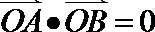
正确答案
(1)由圆方程配方得(x+1)2+(y-3)2=9,
圆心为C(-1,3),
半径为 r = 3,
若 l与C相切,
则得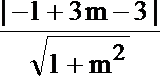
∴(3m-4)2=9(1+m2),
∴m =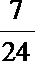
(2)假设存在m满足题意。
由
(m2+1)y2-(8m+6)y+16=0,
由△=(8m+6)2-4(m2+1)·16>0,
得m>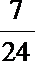
设A(x1,y1),B(x2,y2),
则y1+y2=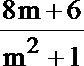
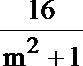
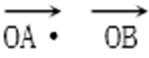
=(3-my1)(3-my2)+y1y2
=9-3m(y1+y2)+(m2+1)y1y2
=9-3m·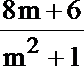
=25-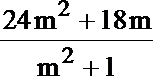
24m2+18m=25m2+25,m2-18m+25=0,
∴m=9±2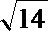
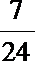
∴存在m=9±2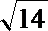
解析
解析已在路上飞奔,马上就到!