理科数学郑州市2014年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

2．已知点和点(1,1)在直线的两侧,则的取值范围是（）

B(-1,8)

C(-8,1)

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

其它不等式的解法

题型：单选题

分值: 5分

3．在△ABC中，若,, ,则角的大小为（）

C或

D或

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦定理

题型：单选题

分值: 5分

4．某观察站与两灯塔、的距离分别为300米和500米，测得灯塔在观察站北偏东30，灯塔在观察站正西方向，则两灯塔、间的距离为（）

A500米

B600米

C700米

D800米

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

解三角形的实际应用

题型：单选题

分值: 5分

6．设是公比为的等比数列，令，若数列的连续四项在集合中，则等于( )

C或

D或

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式等比数列的基本运算

题型：单选题

分值: 5分

7. 若直线通过点，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质恒过定点的直线

题型：单选题

分值: 5分

9．若关于的不等式在区间上有解，则实数的取值范围为（）

C(1,+∞)

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

一元二次不等式的解法

题型：单选题

分值: 5分

10．设正实数满足,则当取得最大值时，的最大值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：单选题

分值: 5分

11．已知数列为等差数列，若且它们的前项和有最大值，则使得的的最大值为（）

A16

B17

C18

D19

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：单选题

分值: 5分

8. 已知，满足约束条件若的最小值为，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

其它不等式的解法

题型：单选题

分值: 5分

1．若，且，则下列不等式一定成立的是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：单选题

分值: 5分

5．在中，若，则是（）

A锐角三角形

B直角三角形

C钝角三角形

D无法确定

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两角和与差的正切函数

题型：单选题

分值: 5分

12. 把正整数排列成如图甲的三角形数阵，然后擦去第偶数行的奇数和第奇数行中的偶数，得到如图乙的三角数阵，再把图乙中的数按从小到大的顺序排成一列，得到数列，若，则的值为（）

A1029

B1031

C1033

D1035

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式等差数列的基本运算归纳推理进行简单的合情推理

填空题本大题共4小题，每小题5分，共20分。把答案填写在题中横线上。

题型：填空题

分值: 5分

13．已知函数.项数为27的等差数列满足，且公差.若，则当=_____时，.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 5分

14．在锐角三角形ABC，A、B、C的对边分别为a、b、c，，则=____________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：填空题

分值: 5分

16．已知，，若对任意总存在，使成立，则实数的取值范围是_____________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 5分

15．若正数满足，则的最小值为_____________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用基本不等式求最值

简答题（综合题）本大题共70分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

20.在数列中，

（1）设求数列的通项公式;

（2）求数列的前项和。

正确答案

解：（1）由已知得且，即，

，

又，所求数列的通项公式为；

（2）由（1）知

令①

则②

①-②得，

，

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：简答题

分值: 12分

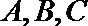
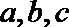
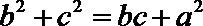
18.在△ABC中，角的对应边分别是满.

（I）求角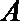的大小；

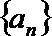
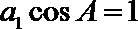
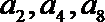
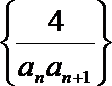
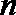
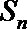
（II）已知等差数列的公差不为零，若，且成等比数列,求的前项和.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：简答题

分值: 12分

19．在中，角所对的边分别为且满足

（1）求角的大小；

（2）求的最大值，并求取得最大值时角的大小．

正确答案

解析：（1）由正弦定理得因为

所以

（2）=

又，

所以

即时取最大值2．

综上所述，的最大值为2

此时

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：简答题

分值: 12分

21. 某人上午7：00乘汽车以千米/小时匀速从A地出发到距300公里的B地，在B地不作停留，然后骑摩托车以千米/小时匀速从B地出发到距50公里的C地，计划在当天16：00至21：00到达C地。设乘汽车、骑摩托车的时间分别是x,y小时，如果已知所需的经费元，那么分别是多少时走的最经济，此时花费多少元？

正确答案

解：由题意得，，

∵ ∴

由题设中的限制条件得，

于是得约束条件

目标函数

做出可行域（如图），

当平行移动到过（10，4）点时纵截距最大，此时最小.

所以当，即时，元

解析

解析已在路上飞奔，马上就到！

知识点

其它不等式的解法不等式的综合应用

题型：简答题

分值: 12分

22. 已知为单调递增的等比数列，且，，是首项为2，公差为的等差数列，其前项和为.

（1）求数列的通项公式；

（2）当且仅当，，成立，求的取值范围.

正确答案

解：（1）因为为等比数列，所以

所以所以为方程的两根；

又因为为递增的等比数列，所以从而，

所以；

（2）由题意可知：，，

由已知可得：，所以，

当且仅当，且时，上式成立，

设，则，

所以，

所以的取值范围为.

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：简答题

分值: 10分

17．已知，不等式的解集是．

（1）求的解析式；

（2）若对任意，不等式恒成立，求t的取值范围．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法一元二次不等式的解法不等式恒成立问题

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷