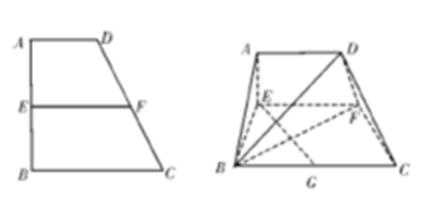- 真题试卷
- 模拟试卷
- 预测试卷
3.已知某随机变量X的概率密度函数为P(x)=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.定义在R上的函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知F是双曲线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.受全球金融危机和国家应对金融危机政策的影响,某公司2012年一年内每天的利润





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.如图,已知三棱锥的底面是边长为l的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数y=f(x)是定义在R上的增函数,函数y=f(x-1)的图象关于点(1,0)对称,若任意的x,y∈R,不等式f(x2-6x+21)+f(y2-8y)<0恒成立,则当x>3时,x2+y2的取值范围是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知函数,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.为加紧调集大量救灾物质支援灾区的救灾工作,某工作人员对6辆货运省汽车进行编组调度,决定将这6辆汽车编成两组,每组3辆,且甲与乙两辆汽车不在同一小组.如果甲所在小组3辆汽车先开出,那么这6辆汽车先后不同的发车顺序共有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知向量



(1)若
(2)若向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知梯形A
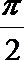
(1)当x=2时,求证:BD⊥EG;
(2)若以F、B、c、D为顶点的三棱锥的体积记为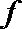
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.对于数列













(1)试问


(2)设






(3)在(2)的条件下,若数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设椭圆






(1)若过



(2)在(1)的条件下,过右焦点







正确答案
解:(1)由题意




所以


所以


又过

所以

所求椭圆方程为
解析
解析已在路上飞奔,马上就到!
知识点
18.某学生社团在对本校学生学习方法开展问卷调查的过程中发现,在回收上来的1000份有效问卷中,同学们背英语单词的时间安排共有两种:白天背和晚上临睡前背。为研究背单词时间安排对记忆效果的影响,该社团以5%的比例对这1000名学生按时间安排类型进行分层抽样,并完成一项实验,实验方法是,使两组学生记忆40个无意义音节(如XIQ、GEH),均要求在刚能全部记清时就停止识记,并在8小时后进行记忆测验。不同的是,甲组同学识记结束后一直不睡觉,8小时后测验;乙组同学识记停止后立刻睡觉,8小时后叫醒测验。两组同学识记停止8小时后的准确回忆(保持)情况如图(区间含左端点而不含右端点)
(1)估计1000名被调查的学生中识记停止后8小时40个音节

(2)从乙组准确回忆因结束在[12,24)范围内的学生中随机选3人,记能准确回忆20个以上(含20)的人数为随机变量X,求X分布列及数学期望;
(3)从本次实验的结果来看,上述两种时间安排方法中哪种方法背英语单词记忆效果更好? 计算并说明理由。
正确答案
解:(1)∵

∴乙组有20人.又∵
∴识记停止8小时后40个音节的保持率大于等于60%的在甲组中有1人,
乙组有
∴
(2)由乙图知,乙组在

在

∴




∴

(3)甲组学生准确回忆音节数共有:

乙组学生准确回忆音节数共有:

解析
解析已在路上飞奔,马上就到!
知识点
21.设函数


(Ⅰ)当

(Ⅱ)若


(Ⅲ)设

正确答案
解:(Ⅰ)


当





∴函数


(Ⅱ)由题

∵


若




不等式


令

又令



①当



∴


∴


②当

ⅰ)若




∴


∴



ⅱ)若





∴


∴

综上,不等式


(Ⅲ)由(Ⅱ)知,当

当

令

∴


又由(Ⅰ)得

当x>0时,
∴

综上得

解析
解析已在路上飞奔,马上就到!
知识点
22.(选修4—5:不等式选讲)
已知函数
(1)若不等式

(2)当a
正确答案
(1)解:由

所以

(2)解:当


①当

当
解之得



综上,当



解析
解析已在路上飞奔,马上就到!
知识点
12.为调查某市中学生平均每人每天参加体育锻炼时间(单位:分钟),按锻炼时间分以下四种情况统计:①0~10分钟;②11~20分

正确答案
0.38
解析
解析已在路上飞奔,马上就到!
知识点
11.地面上有三个同心圆(如图),


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.请从(1),(2),(3)中选做一道
(1)(几何证明选讲)
如图,圆0的割线PBA过圆心O,弦CD交PA于
(2)(坐标系与参数方并呈)
极坐标系中,曲线
(3)(不等式选讲)
已知半圆的直径AB=2R,P是弧AB上一点,则2|PA|+3|PB|的最大值是________.
正确答案
(1)3;
(2)
(3)
解析
解析已在路上飞奔,马上就到!
知识点
13.定义:称





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知数集X={



①向量(

②向量(

③向量(

(1)若{1,3,x}具有性质P,则x的取值为________.
(2)若数集{l,3

正确答案
(1)

(2)
解析
解析已在路上飞奔,马上就到!