- 真题试卷
- 模拟试卷
- 预测试卷
2.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.定义运算
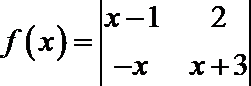
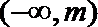
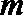
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知命题





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已若当




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.下列命题中,真命题是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知正实数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数






正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
15.给出下列命题:
①若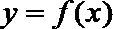
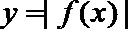
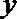
②若函数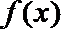

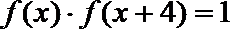
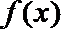
③若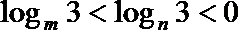
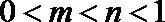
④若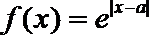
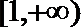
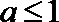
其中正确命题的序号是( )
正确答案
①②④
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数
(1)判断函数
(2)是否存在实数


正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
18.设函数


(1)求
(2)当


正确答案
(1)
因为函数




即
解得

(2)当



又因为
解析
解析已在路上飞奔,马上就到!
知识点
19.已知一企业生产某产品的年固定成本为10万元,每生产千件需另投入2.7万元,设该企业年内共生产此种产品

(1)写出年利润

(2)年产量为多少千件时,该企业生产此产品所获年利润最大?(注:年利润=年销售收入-年总成本)
正确答案
(1)当
当
(2)①当









②当
当且仅当

综合①、②知

所以当年产量为9千件时,该企业生产此产品获利最大
解析
解析已在路上飞奔,马上就到!
知识点
16.已知全集U=R,集合


正确答案
A={
={



B={





∴




(



解析
解析已在路上飞奔,马上就到!
知识点
20.定义在



(1)求证:
(2)若


正确答案
(1)证明:
令

令

则有


所以
(2)解:



所以

又由(1)


(法一):令


令

当


当

解得
综上所述当


(法二):分离
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(1)求
(2)若方程



(3)令








正确答案
(1)

解得
(2)
则
令

当



当



于是方程


即
(3)由题意
假设结论不成立,则有:
①-②,得
由④得


令


解析
解析已在路上飞奔,马上就到!