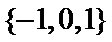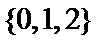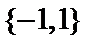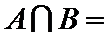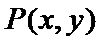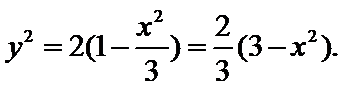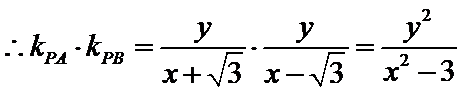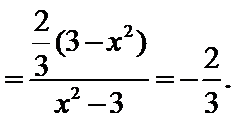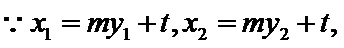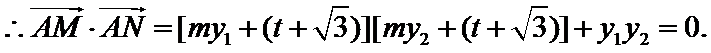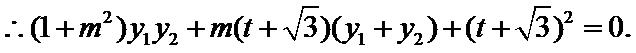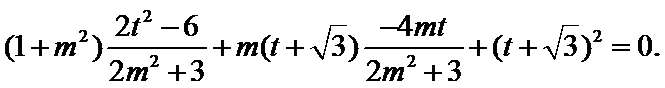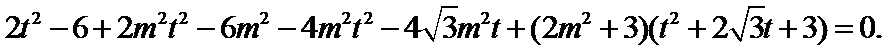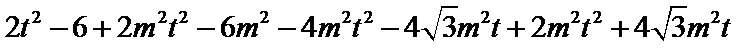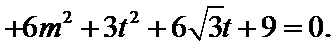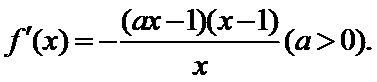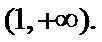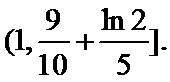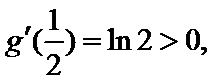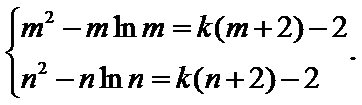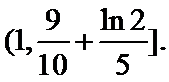- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合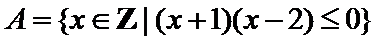
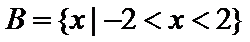
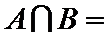
正确答案
解析
因为集合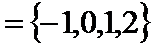
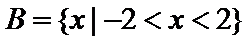
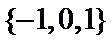
考查方向
解题思路
先求出集合A,再与集合B取交集。
易错点
集合A中的元素是整数,容易忽略;集合的交集是取两个集合的公共部分。
知识点
2.在


正确答案
解析
因为


因为

考查方向
解题思路
先由

易错点
本题易在由

知识点
3.如图为一个半球挖去一个圆锥后的几何体的三视图,则剩余部分与挖去部分的体积之比为( )
正确答案
解析
由三视图可得,半球的半径为2,圆锥的底面半径和高都等于2,所以半球的体积为



考查方向
解题思路
由三视图先分别求出半球和圆锥的体积,再求出剩余部分的体积,即可求出体积比。
易错点
本题易在求半球的体积时发生错误。
知识点
8.过双曲线



正确答案
解析
设直线AC的方程为

由

由






考查方向
解题思路
设出过点


易错点
求直线与双曲线的渐近线交点时,发生错误。
知识点
4.设


正确答案
解析
因为





考查方向
解题思路
先分别
易错点
本题易在比较a, b时出错。
知识点
5.已知

正确答案
解析
对于选项A


对于选项C,直线

考查方向
解题思路
根据选项逐个进行分析、判断。
易错点
对线面、面面的平行或垂直的判定定理理解不透彻,导致出错。
知识点
6.执行如图所示程序框图,若使输出的结果不大于50,则输入的整数
正确答案
解析
由题可得
则

考查方向
解题思路
根据输出的结果不大于50,来求
易错点
对判断条件理解不清楚或计算S的值时出错。
知识点
7.已知菱形





正确答案
解析





考查方向
解题思路
画出图形,分别把

易错点
不会利用向量加法的几何意义运算或进行向量的数量积运算时,夹角出错,
知识点
9.设不等式组





正确答案
考查方向
易错点
1、画可行域时易出错;
知识点
10.如果数列

















(参考数据:

正确答案
解析
由












所以数列









考查方向
解题思路
先利用条件求出数列


易错点
不会利用向量加法的几何意义运算或进行向量的数量积运算时,夹角出错,
知识点
12.

正确答案
-280
解析
由题意可得

考查方向
解题思路
写出通项公式,令
易错点
本题易在利用通项公式时发生错误。
知识点
11.设复数



正确答案
解析
因为

考查方向
解题思路
根据复数的基本运算,进行化简即可。
易错点
本题易在复数的乘除时发生错误。
知识点
13.甲、乙两人在5次综合测评中成绩的茎叶图如图所示,其中一个数字被污损,记甲,乙的平均成绩分别为


正确答案
解析
由已知题中的茎叶图,可得乙的5次综合测评中的成绩分别为87,86,92,94,91,则乙的平均成绩:












考查方向
解题思路
先设污损数字为



易错点
本题易在求被污损数字的范围时发生错误 。
知识点
15.已知函数





正确答案
解析
由于对数函数























考查方向
解题思路
由于对数函数








易错点
求实数

知识点
14.如图,某房地产公司要在一块矩形宽阔地面上开发




正确答案
解析
根据题意,当开发面积最大时,三角形OMN的面积就最小。设直线MN与曲线相切于点




令




当且仅当



考查方向
解题思路
先设切点的坐标,并运用导数得出切线方程,再求出直线的横纵截距,最后运用基本不等式求出
易错点
本题易在利用基本不等式求最值或用导研究函数最值时发生错误 。
知识点
已知等比数列


16.求
17.若



正确答案
解析
【解析】
由题意,得



考查方向
解题思路
解题步骤如下:根据等比数列的通项公式化简等式

易错点
本题在求等比数列的公比或求数列


正确答案
解析
【解析】



考查方向
解题思路
解题步骤如下:因为





易错点
本题在求等比数列的公比或求数列


如图,菱形




且
22.求证:

23.若

正确答案
见解析
解析
如图,过点





















考查方向
解题思路
解题步骤如下:做辅助线:过点







平面

易错点
本题易在利用面面垂直证明线面垂直或求法向量时发生错误 。
正确答案
二面角

解析
连接








则


设平面


令

设平面


令




考查方向
解题思路
解题步骤如下:建立空间直角坐标系,根据题目给出的条件,分别求出平面



易错点
本题易在利用面面垂直证明线面垂直或求法向量时发生错误 。
已知向量m



20.求函数

21.设






正确答案
当

解析








考查方向
解题思路
解题步骤如下:利用向量的坐标运算、倍角公式、辅助角公式把函数



易错点
本题易在利用倍角公式变形时发生错误 。
正确答案
解析
由题意,得





考查方向
解题思路
解题步骤如下:由



易错点
本题易在利用倍角公式变形时发生错误 。
已知椭圆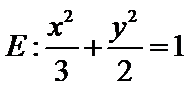
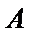
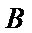
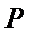
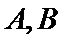
24.求直线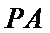
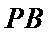

25.设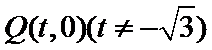

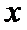
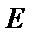

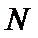
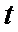
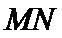
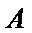

正确答案
直线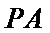
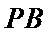
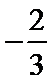
解析
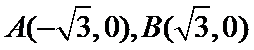
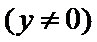
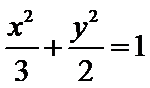
考查方向
解题思路
解题步骤如下:由椭圆的方程,可得到A ,B两点的坐标,设出点P(x,y),即可表示出直线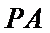
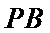
易错点
本题是综合性比较强的大题,涉及到的的知识点比较多,计算量较大,所以在计算时易发生错误 。
正确答案
存在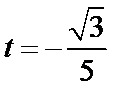
解析
【解析】令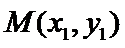
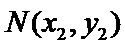
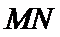
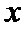
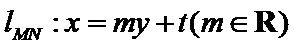
由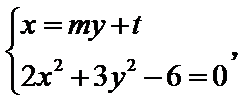
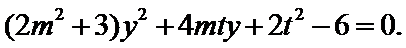
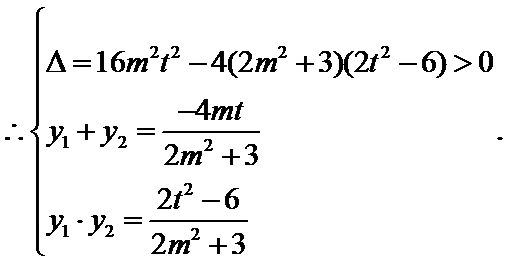
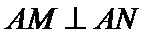
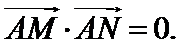
将(*)式代入上式,得
即
展开,得
整理,得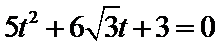
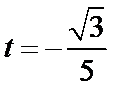
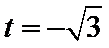
经检验,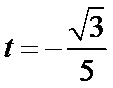
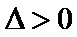
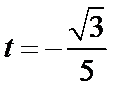
考查方向
解题思路
解题步骤如下:要满足以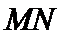

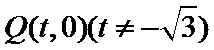
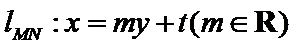
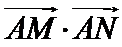
易错点
本题是综合性比较强的大题,涉及到的的知识点比较多,计算量较大,所以在计算时易发生错误 。
某类题库中有9道题,其中5道甲类题,每题10分,4道乙类题,每题5分.现从中任意选取三道题组成问卷,记随机变量
18.求
19.求

[来源:学+科+网]
正确答案
见解析。
解析
【解析】由题意,
∵

∴
[来源:学科网ZXXK]
考查方向
解题思路
先求出随机变量
易错点
本题易在求分布列时发生错误。
正确答案

解析
【解析】
考查方向
解题思路
先求出随机变量
易错点
本题易在求分布列时发生错误。
已知函数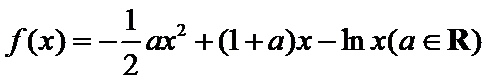
26.当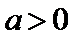
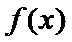
27.当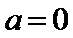
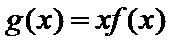
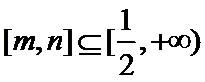
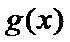
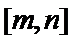

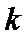

正确答案
当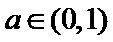
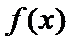
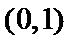
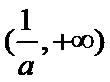
当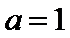

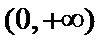
当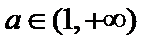
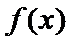

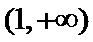
解析
【解析】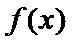
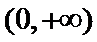
①当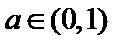
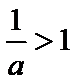
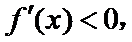
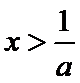
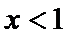
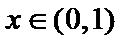
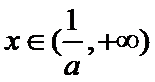
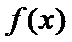
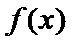
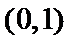
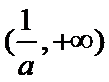
② 当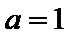
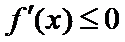
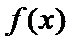
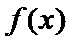
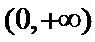
③ 当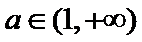
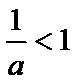
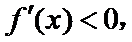
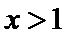
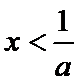
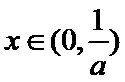
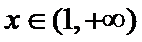
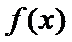
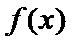
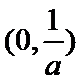
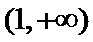
综上,当
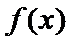
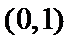
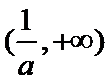
当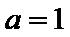
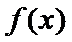
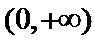
当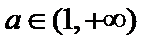
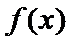
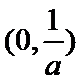
考查方向
解题思路
解题步骤如下:先求函数的导数,根据导函数的正负来讨论原函数的单调性,注意讨论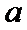
易错点
本题易在分类讨论和解含参数的不等式时发生错误 。
正确答案
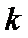
解析
当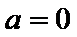
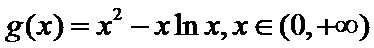
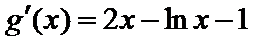
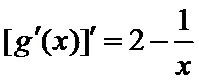
当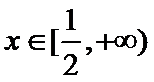
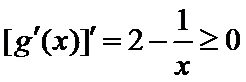
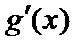
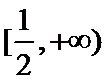
又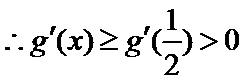

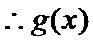
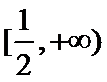
由题意,得
原问题转化为关于
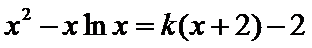
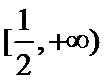
即方程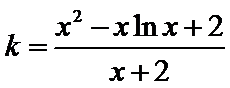
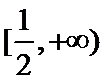
令函数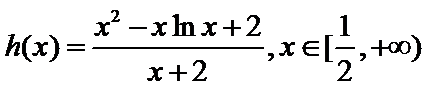
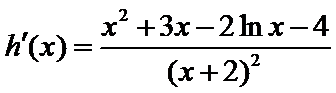
令函数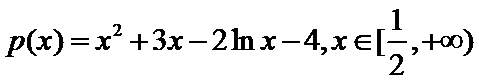
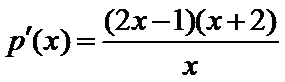
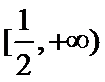
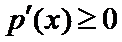
故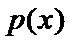
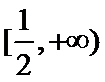
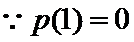
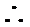
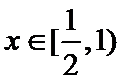
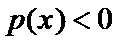
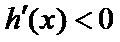
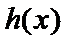
当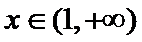

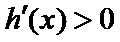
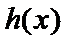
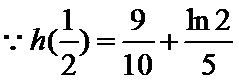
考查方向
解题思路
解题步骤如下:根据函数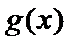
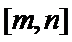
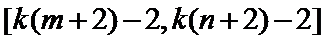
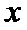
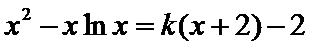
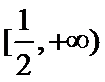
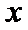

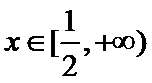
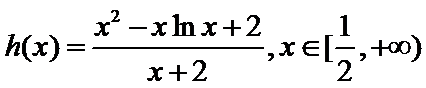
易错点
本题不容易构造函数,讨论其单调性,求其范围,导致题目无法进行。