- 真题试卷
- 模拟试卷
- 预测试卷
2.设z=1+i (i是虚数单位),则

正确答案
解析

考查方向
本题主要考查复数的运算
解题思路
1、求出
2、计算

易错点
本题易在求共轭复数时发生错误。
知识点
4.函数f(x)=
正确答案
解析

考查方向
本题主要考查导数的几何意义
解题思路
1、求出f(x)的导数;
2、代入求值,即可得到结果。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在求导数时发生错误,易用错运算法则。
知识点
5.已知函数f(x)=
正确答案
解析
由图可知,2个函数图像有3个交点。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
本题主要考查函数图像及零点
解题思路
1、分别画出2个函数图像;
2、求出交点个数,即可得到结果。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在画图时发生错误。
知识点
6.按如下程序框图,若输出结果为273,
正确答案
解析
由题可知,S=0+31+33+35=273,得i=7。A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
本题主要考查流程图
解题思路
按照流程图所示依次代入计算,即可得到结果。A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在判断循环次数时发生错误。
知识点
7.设双曲线

同,则此双曲线的方程为
正确答案
解析
由c=1,且焦点在y轴上,得a=2b。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
本题主要考查双曲线的标准方程
解题思路
1、求出c;
2、利用a,b,c关系求a,b,即可得到结果。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在判断焦点位置时发生错误。
知识点
10.已知函数f(x)=x+




f(x1)≥g(x2),则实数a的取值范围是
正确答案
解析
f(x)min=f(1)=5, g(x)min = g(2)=4+a,得a≤1。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
本题主要考查函数的值域
解题思路
1、求出f(x)在[
2、求出f(x)min≥g(x)min,即可得到结果。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在判断范围大小时发生错误。
知识点
11.已知椭圆
正确答案
解析
设F1A=x, F2A=y,由题可知,x+y=2a,x2+y2=4c2,2x+√2x=4a,联立方程组,代换得
a2(9-6√2)=c2,即e=

考查方向
本题主要考查直线与椭圆的位置关系
解题思路
1、用a,c表示出F1A,F2A;
2、将所求式子联立,即可得到结果。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在表示a, c关系时发生错误。
知识点
3.在△ABC中,角A,B,C所对的边分别为a,b,c,若

正确答案
解析

考查方向
本题主要考查解三角形的正弦定理
解题思路
利用正弦定理求解,即可得到结果。A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在代换时发生错误。
知识点
8.正项等比数列{

正确答案
解析

考查方向
本题主要考查极值和数列、对数运算
解题思路
1、求出a1,a4031;
2、求出a2016,即可得到结果。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在求a2016时发生错误。
知识点
9.图是一个四面体的三视图,这三个视图均是腰长为2的等腰直角三角形,正视图和俯视图中的虚线是三角形的中线,则该四面体的体积为
正确答案
解析
由图可知,此几何体为底边长分别为1,2,高为2的三棱锥。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
本题主要考查三视图
解题思路
1、还原几何体;
2、求出体积,即可得到结果。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在还原几何体时发生错误。
知识点
12.已知函数f(x)=
正确答案
解析
设f(x)=t,方程 t2+at-b2=0的两根分别为t1、t2,则t1t2=-b2≤0.若b≠0,则t1、t2异号,由函数图像可知,对应的x值不唯一,因此,b=0。即不等式的解为-a<t<0.注意到t=0时x=0,或x=2.因此a的最大值为8。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
本题主要考查分段函数和不等式
解题思路
1、画出f(x)的图像;
2、利用方程只有一个整数解求解,即可得到结果。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在处理只有一个整数解时发生错误。
知识点
1.设全集U={x∈N﹡|x≤4},集合A={1,4},B={2,4},则
正确答案
解析
A∩B={4},
考查方向
本题主要考查集合的交集、补集运算
解题思路
1、求出A∩B;
2、求出
易错点
本题易在求补集时发生错误。
知识点
14.若不等式

正确答案
解析
由题可知SM=2π,SN=48,则P=
考查方向
本题主要考查线性规划及几何概型。
解题思路
解题步骤如下:1、画出平面区域。2、利用概率公式求解.
易错点
本题必须注意利用图像完成。
知识点
15.△ABC的三个内角为A、B、C,若

正确答案
解析
由题可知,A=45o,可求得2cosB+sin2C=2cosB-2cos2B+1≤
考查方向
本题主要考查了三角函数的最值。
解题思路
解题步骤如下:利用两角和差公式求解。
易错点
本题要注意公式的化简。
知识点
17. 已知数列{


(Ⅰ)求数列{
(Ⅱ)若



正确答案
an=4n-3;
解析
⑴解:由已知条件:






⑵解:由⑴可得





考查方向
本题主要考查数列的综合运算
解题思路
1、求出an;
2、利用公式分类讨论,即可得到结果。
易错点
本题易在分类讨论时发生错误。
知识点
21. 设函数f(x)=

(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)当m≥0时,讨论函数f(x)与g(x)图象的交点个数.
正确答案
(1)当






解析
⑴解:函数


当



当

当


当


综上:当














































考查方向
本题考查了利用导数求含参数的函数极值,分类讨论,讨论点大体可以分成以下几类:
1、根据判别式讨论;
2、根据二次函数的根的大小;
3、定义域由限制时,根据定义域的隐含条件;
4、求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论;
5、多次求导求解等.
解题思路
1、求导,然后解导数不等式,求单调区间。
2、对参数分类讨论得结论。
易错点
第二问中的易丢对a的分类讨论。
知识点
13.二项式

正确答案
60
解析
由题可知,Tk+1=C6k(x)6-k-k(-2)k=60x2,可求得系数为60。
考查方向
本题主要考查了二项式定理。
解题思路
解题步骤如下:利用通项公式求解。
易错点
本题要注意通项公式。
知识点
16.已知点A(0,-1),B(3,0),C(1,2),平面区域P是由所有满足


正确答案
解析
由题可知,设M(x,y),则


8<x≤3m+n,7<y≤m+3n-1,画出平面区域,利用面积公式可得(m+n)min=
考查方向
本题主要考查线性规划及向量的线性运算。
解题思路
1、画出平面区域
2、化简公式求解.
易错点
本题必须注意利用图像完成。
知识点
18.某中药种植基地有两处种植区的药材需在下周一、周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘.由于下雨会影响药材品质,基地收益如下表所示:
若基地额外聘请工人,可在周一当天完成全部采摘任务.无雨时收益为20万元;有雨时收益为10万元.额外聘请工人的成本为a万元. 已知下周一和下周二有雨的概率相同,两天是否下雨互不影响,基地收益为20万元的概率为0.
(Ⅰ)若不额外聘请工人,写出基地收益X的分布列及基地的预期收益;
(Ⅱ)该基地是否应该外聘工人,请说明理由.
正确答案
(1)14.4;
(2)当额外聘请工人的成本高于1.6万元时,不外聘工人;成本低于1.6万元时,外聘工人;成本恰为1.6万元时,是否外聘工人均可以.
解析
本题属于概率统计中的基本问题,题目的难度是逐渐由易到难.
⑴解:设下周一有雨的概率为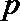
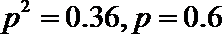
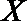
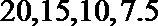
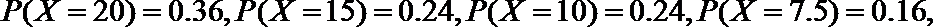
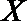

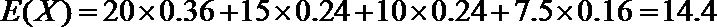
⑵设基地额外聘请工人时的收益为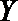
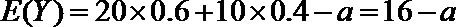
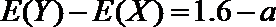
考查方向
本题考查了概率统计中的离散型随机变量的分布列和数学期望的问题.属于高考中的高频考点。
解题思路
1、写出随机变量的取值,并求出相应的概率和数学期望。
2、利用已知分类讨论。
易错点
随机变量的取值及对应的概率。
知识点
19. 如图,矩形CDEF和梯形ABCD互相垂直,∠BAD=∠ADC=90°,AB=AD=
(Ⅰ)若M为EA中点,求证:AC∥平面MDF;
(Ⅱ)求平面EAD与平面EBC所成锐二面角的大小.
正确答案
(1)略;(2)60O.
解析
⑴证明:设



在矩形


因为

所以

又因为



所以

⑵解:因为平面






所以

以
设


因为
所以

设平面




注意到平面

所以,平面


考查方向
本题考查了立体几何中的线面平行和二面角的问题.属于高考中的高频考点。
解题思路
1、转化为证明线线平行
2、建立空间直角坐标系,利用夹角的余弦公式求解。
易错点
1、第一问中的线面平行的转化。
2、第二问中二面角求解时要建立适当的空间直角坐标系。
知识点
20. 已知点M(-1,0),N(1,0),曲线E上任意一点到点M的距离均是到点N距离的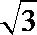
(Ⅰ)求曲线E的方程;
(Ⅱ)已知m≠0,设直线l1:x-my-1=0交曲线E于A,C两点,直线l2:mx+y-m=0交曲线E于B,D两点.C,D两点均在x轴下方.当CD的斜率为-1时,求线段AB的长.
正确答案
(1)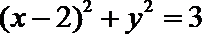
(2)线段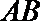
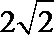
解析
⑴解:设曲线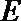
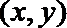
由题意,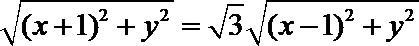
整理得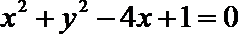
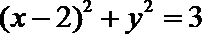
⑵解:由题知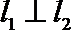
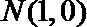
设曲线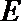
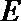
则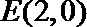
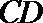
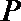
则直线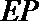
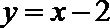
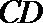
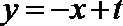
由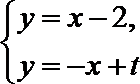
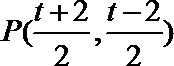
由圆的几何性质,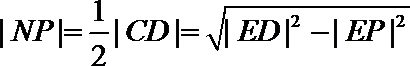
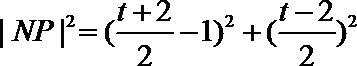
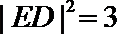
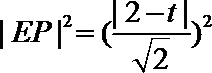
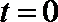
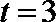
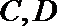
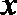
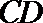
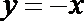
解得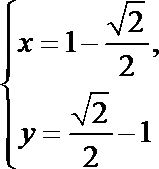

设
由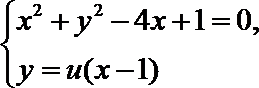

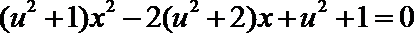
⑴ 方程⑴的两根之积为1,
所以点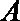
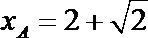
又因为点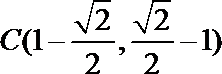
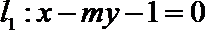
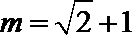
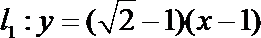
所以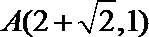
同理可得,
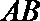
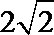
考查方向
本题考查了圆的标准方程和直线与圆的位置关系,属于高考中的高频考点.
解题思路
1、利用已知求解。
2、联立直线与圆方程求解。
易错点
第二问中表示直线斜率时容易出错。
知识点
本题为选做题,请考生在第22、23、24三题中任选一题做答。如果多做。则按所做的第一题记分.作答时用2B铅笔在答题卡上把所选题目的题号涂黑.
22.选修4—l:几何证明选讲如图,∠BAC的平分线与BC和△ABC的外接圆分别相交于D和E,延长AC交过D、E、C三点的圆于点F.(Ⅰ)求证:EC=EF;(Ⅱ)若ED=2,EF=3,求AC·AF的值.
23.选修4—4:坐标系与参数方程 已知曲线C1的参数方程为


24.选修4—5:不等式选讲 已知函数f(x)=|x-2|-|x+1|.(Ⅰ)解不等式f(x)>1;(Ⅱ)当x>0时,函数g(x)=
正确答案
22.略.
23.(1)

24.(1)

解析
22. ⑴证明:因为





⑵解:因为






23. ⑴解:




⑵解:








24.⑴解:当








⑵解:因为






考查方向
22.本题考查了平面几何的知识,主要涉及直线与圆的位置关系,三角形相似的考查.
23.本题考查了参数方程的知识,主要涉及直线与圆的位置关系.
24.本题考查了不等式的知识,主要涉及绝对值不等式的解法
解题思路
22解题步骤如下:1、利用圆的相关定理证明。2、利用切割线定理和相交弦定理证明。
23解题步骤如下:1、利用公式消参。2、可以利用普通方程求解。
24.解题步骤如下:1、利用公式解绝对值不等式。2、可以利用图像求解。
易错点
22.相关的定理容易混用。
23.消参的过程容易出错。
24.去绝对值时容易出错。