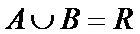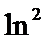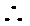- 真题试卷
- 模拟试卷
- 预测试卷
1.复数z为纯虚数,若
正确答案
解析





知识点
3.某防疫站对学生进行身体健康调查,欲采用分层抽样的办法抽取样本.某中学共有学生2000名,抽取了一个容量为200的样本,样本中男生103人,则该中学共有女生( )
正确答案
解析
抽取比例为

知识点
4.设

正确答案
知识点
5.下列四个结论中正确的个数是( )
①“

②命题:“

③“若
④若

正确答案
解析
①项是必要不充分条件,③项逆命题是:若

④项
知识点
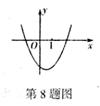
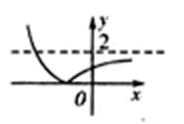
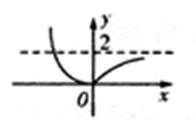
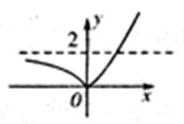
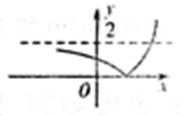
8.已知a是常数,函数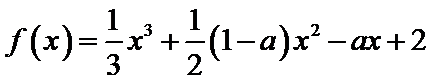
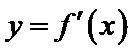
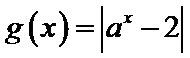
正确答案
解析
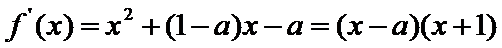
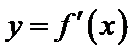
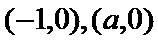
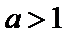
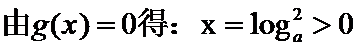
知识点
2.已知集合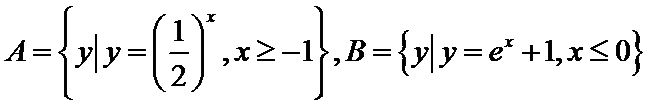
正确答案
解析
集合A、B简化为: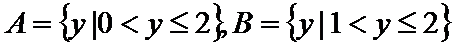
知识点
6.若执行右边的程序框图,输出S的值为
正确答案
解析
第一次循环:





知识点
7.在



正确答案
解析
将







知识点
10.设双曲线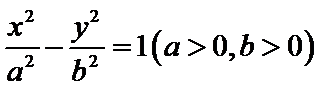
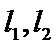
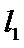

正确答案
解析
过F和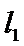
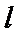
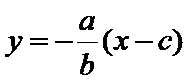
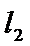
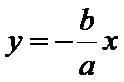
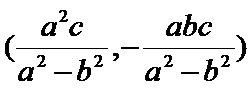
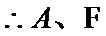
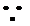
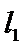
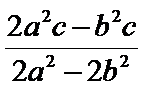
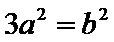
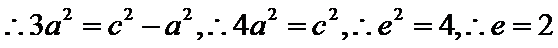
知识点
9.若


正确答案
解析







知识点
11.已知

正确答案
解析



知识点
12.若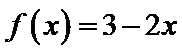
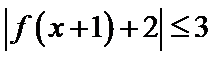
正确答案
解析
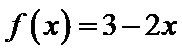
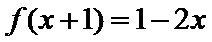

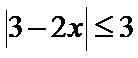
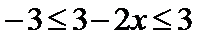
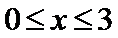
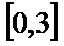
知识点
13.已知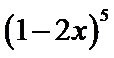
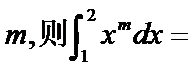
正确答案
解析
令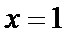
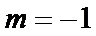
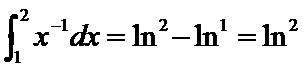
知识点
14.在三棱柱



正确答案
解析
本题主要考查了三棱柱的体积的求解,解题步骤如下:
考查方向
本题主要考查了三棱柱的体积/几何体的体积计算是高考中的热点,主要涉及有三视图求体积、顶点转换法求三棱锥的体积,属于中档题。
易错点
不能将三棱柱正确的分割为几个可以求体积的几何体。
知识点
15.已知实数



正确答案
解析






考查方向
本题主要考查了基本不等式求最值。
易错点
知识点

若抽签结果为甲组:

22.求c获得第1名的概率;
23.求c的名次X的分布列和数学期望.
正确答案
解析
考题分析:本题是概率问题中的基本问题,比较简单,(1)相互独立事件的概率按公式计算就可,注意有些比较复杂的事件,我们通常把它分成几个彼此互斥的事件或考虑对立事件;(2)分布列是解决期望和方差的基础,随机变量的所有取值是关键。
考查方向
本题主要考查了概率和分布列及期望/考查运用概率知识解决实际问题的能力,相互独立事件是指两事件发生的概率互不影响,注意应用相互独立事件同时发生的概率公式.
解题思路
本题主要考查了概率和分布列及期望,解题步骤如下:1、将c获得第一分为两个互斥事件:一个是在他的分组中获胜,二是和另一组中胜者比赛时也获胜,分别求两个互斥事件的概率再相加即可。2、c获得名次的所有可能取值为1、2、3、4分别计算概率,求期望和列分布列。
易错点
随机变量的所有取值找不全,有遗漏。
正确答案
EX=
解析
考题分析:本题是概率问题中的基本问题,比较简单,(1)相互独立事件的概率按公式计算就可,注意有些比较复杂的事件,我们通常把它分成几个彼此互斥的事件或考虑对立事件;(2)分布列是解决期望和方差的基础,随机变量的所有取值是关键。
考查方向
本题主要考查了概率和分布列及期望/考查运用概率知识解决实际问题的能力,相互独立事件是指两事件发生的概率互不影响,注意应用相互独立事件同时发生的概率公式.
解题思路
本题主要考查了概率和分布列及期望,解题步骤如下:1、将c获得第一分为两个互斥事件:一个是在他的分组中获胜,二是和另一组中胜者比赛时也获胜,分别求两个互斥事件的概率再相加即可。2、c获得名次的所有可能取值为1、2、3、4分别计算概率,求期望和列分布列。
易错点
随机变量的所有取值找不全,有遗漏。
已知函数
24.若
25.设


正确答案
解析
本题主要考查导数的应用,试题较难,(1)涉及恒成立问题,转化成求函数的最值,这种思路是一般解法,往往要利用“分离参数法”.涉及对数函数,要特别注意函数的定义域.(2)不等式证明:通常构造函数,通过求函数最值解决。
考查方向
本题主要考查了导数的应用:求最值、证明不等式/导数的应用是每年高考必考内容,属于压轴题,较难,主要考查:讨论单调性、存在或恒成立求参数、求最值及极值、证明不等式、研究函数零点等。
解题思路
本题主要考查了导数的应用:求最值、证明不等式,解题步骤如下:1、分离参数a,求函数最值;
易错点
分离参数a 时,要在不等式两边同时除以x,忽视x>0。
正确答案
(见解析)
解析
本题主要考查导数的应用,试题较难,(1)涉及恒成立问题,转化成求函数的最值,这种思路是一般解法,往往要利用“分离参数法”.涉及对数函数,要特别注意函数的定义域.(2)不等式证明:通常构造函数,通过求函数最值解决。
考查方向
求最值、证明不等式/导数的应用是每年高考必考内容,属于压轴题,较难,主要考查:讨论单调性、存在或恒成立求参数、求最值及极值、证明不等式、研究函数零点等。
解题思路
易错点
已知函数
① 周期
②图象向左平移
③
16.求函数
17.设

正确答案
解析
试题分析:本题主要考查了由三角函数性质求解析式和三角恒等变换求值,试题难度较小。(1)利用方程思想分别依次求出


正确答案
解析
试题分析:本题主要考查了由三角函数性质求解析式和三角恒等变换求值,试题难度较小。(1)利用方程思想分别依次求出





考查方向
本题主要考查了由三角函数性质求解析式和三角恒等变换求值。
解题思路
易错点
第一问向左平移时忽视x的系数而出错,第二问不能准确的确定好角的范围。
如图,在四棱锥



18.求证:
19.求直线MN与平面PCD所成角的正弦值.
正确答案
(见解析)
解析
试题分析:本题是立体几何中的常见问题,试题难度不大,(1)需要作辅助线:取CD的中点N,连接AN,PN,证明
考查方向
本题主要考查了线面垂直的证明以及线面角/考查了学生空间想象能力以及逻辑思维能力。
解题思路
易错点
利用向量法求线面角时,忽视向量夹角(或补角)与线面角互为余角。
正确答案
解析
试题分析:本题是立体几何中的常见问题,试题难度不大,(1)需要作辅助线:取CD的中点N,连接AN,PN,证明
考查方向
本题主要考查了线面垂直的证明以及线面角/考查了学生空间想象能力以及逻辑思维能力。
易错点
利用向量法求线面角时,忽视向量夹角(或补角)与线面角互为余角。
已知正项数列




20.求数列
21.符号





正确答案
解析
试题分析:已知


考查方向
本题主要考查了数列求通项公式和数列求和/各省市高考题几乎必考,一般有二问设置,第一问求通项,第二问求和。
解题思路
本题主要考查了数列求通项公式和数列求和,解题步骤如下:1、在给出的an与sn的关系中,令n=n-1得到另一关系式,两式相减,推导出an,an-1的关系,利用等差数列通项公式求出,同理bn
易错点
1、在由递推公式求通项时,忘记验证n=1是否符合,2、错位相减法求和时,忘记在两边同时除以q.
正确答案
解析
试题分析:(1)已知



考查方向
本题主要考查了数列求通项公式和数列求和/各省市高考题几乎必考,一般有二问设置,第一问求通项,第二问求和。
解题思路
本题主要考查了数列求通项公式和数列求和,解题步骤如下:1、在给出的an与sn的关系中,令n=n-1得到另一关系式,两式相减,推导出an,an-1的关系,利用等差数列通项公式求出,同理bn
易错点
1、在由递推公式求通项时,忘记验证n=1是否符合,2、错位相减法求和时,忘记在两边同时除以q.
已知椭圆


26.求椭圆
27.设O为坐标原点,M是直线


若



正确答案
解析
考题分析:本题主要考查了椭圆与圆的方程及直线与圆锥曲线的位置关系,解题过程如下:(1)将条件转化为a、b的方程,解答即可。(2)①设M(2,t),依据弦长一半、半径、弦心距三者满足勾股定理解t;②用t表示圆

考查方向
本题主要考查了椭圆与圆的方程及直线与圆锥曲线的位置关系/圆锥曲线的方程及直线与圆锥曲线的位置关系是高考的必考内容,经常作为压轴题,较难,主要涉及:方程的求解、定值定点问题、最值问题等。
解题思路
本题主要考查了椭圆与圆的方程及直线与圆锥曲线的位置关系,解题步骤如下:1、直接列方程求解即可;
易错点
1、设M的纵坐标为t后,找不到t满足的等式;2、设直线方程时,忘记讨论斜率不存在的情况。
正确答案
(1)

解析
考题分析:本题主要考查了椭圆与圆的方程及直线与圆锥曲线的位置关系,解题过程如下:(1)将条件转化为a、b的方程,解答即可。(2)①设M(2,t),依据弦长一半、半径、弦心距三者满足勾股定理解t;②用t表示圆

考查方向
本题主要考查了椭圆与圆的方程及直线与圆锥曲线的位置关系/圆锥曲线的方程及直线与圆锥曲线的位置关系是高考的必考内容,经常作为压轴题,较难,主要涉及:方程的求解、定值定点问题、最值问题等。
解题思路
易错点
1、设M的纵坐标为t后,找不到t满足的等式;2、设直线方程时,忘记讨论斜率不存在的情况。