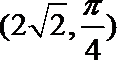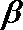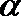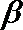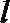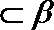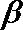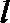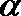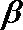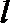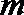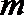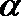- 真题试卷
- 模拟试卷
- 预测试卷
1.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知线性方程组的增广矩阵为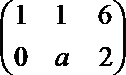

则实数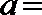
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.中心在原点,焦点在x轴上的双曲线的一条渐近线为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.执行如下图所示的程序框图,若输入

正确答案
23
解析
解析已在路上飞奔,马上就到!
知识点
4.若
是( ) 。
正确答案
180
解析
解析已在路上飞奔,马上就到!
知识点
5.已知集合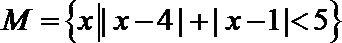
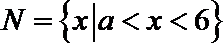
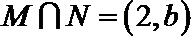
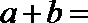
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.有一个正四面体的棱长为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.正项等比数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知曲线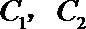

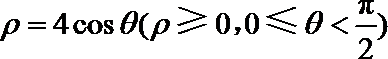

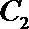
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.如图,矩形









正确答案
216
解析
解析已在路上飞奔,马上就到!
知识点
12.若




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数
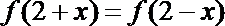
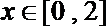

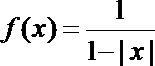
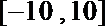
正确答案
9
解析
解析已在路上飞奔,马上就到!
知识点
15.若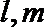
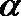

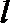
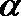
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.圆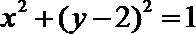
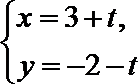
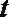
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.某中学高二年级的一个研究性学习小组拟完成下列两项调查:
①从某社区430户高收入家庭,980户中等收入家庭,290户低收入家庭中任意选出170户调查社会购买力的某项指标;
②从本年级12名体育特长生中随机选出5人调查其学习负担情况;
则该研究性学习小组宜采用的抽样方法分别是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,某市准备在道路EF的一侧修建一条运动比赛道,赛道的前一部分为曲线段FBC.该曲线段是函数





(1)求

(2)若要在圆弧赛道所对应的扇形ODE区域内建一个“矩形草坪”,矩形的一边在道路EF上,一个顶点在半径OD上,另外一个顶点P在圆弧

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,





(Ⅰ)若



(Ⅱ)求平面

正确答案
(Ⅰ)证明:连结PC,交DE于N,连结MN,
在△PAC中,M,N分别为两腰PA,PC的中心, ∴ MN//AC,
∵ MN

(Ⅱ)解法一:设平面PAD与PBC所成锐二面角的大小为

P


设平面PAD的单位法向量为
设面PBC的法向量

即:
解得:

∴ 
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)求函数
(2)若

(3)设

正确答案
(1)
(2)
(3)
解析
解析已在路上飞奔,马上就到!
知识点
22.已知椭圆C:



(1)用m表示点E,F的坐标;
(2)证明直线EF与y轴交点的位置与m无关;
(3)若∆BME面积是∆AMF面积的5倍,求m的值.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.设数列





(1)当



(2)当





(3)若数列













正确答案
(1)
(2)
(3)
由(2)知数列

又
得:对任意

得

又由已知,

一方面,当
对任意

另一方面,当


则
取

当


当 

又
∴
解析
解析已在路上飞奔,马上就到!