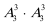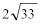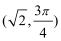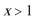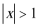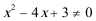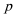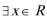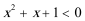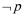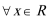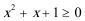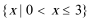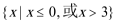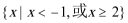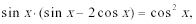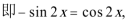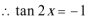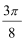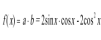- 真题试卷
- 模拟试卷
- 预测试卷
5.若定义在R上的偶函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 对于下列命题:
①已知i是虚数单位,函数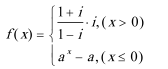
②五本书排成一排,若A、B、C三本书左右顺序一定(不一定相邻),那么不同排法有
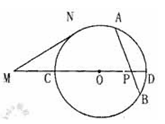
③如图,⊙O中的弦AB与直径CD相交于点p,M为DC延长线上一点,MN为⊙O的切线,N为切点,若AP=8, PB=6, PD=4, MC=6,则MN的长为
④在极坐标系(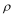
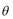
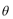
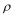
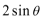

⑤设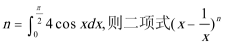
其中假命题的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.下列说法错误的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若向量a、b满足a +b =(2,-1),a =(1,2),则向量a与b的夹角等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 下列函数中,周期为1的奇函数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合S = R,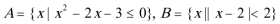
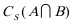
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知△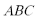
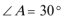
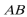
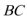
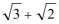

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知数列



正确答案

解析
解析已在路上飞奔,马上就到!
知识点
9.若




正确答案

解析
解析已在路上飞奔,马上就到!
知识点
11.函数


正确答案


解析
解析已在路上飞奔,马上就到!
知识点
13.在正方形ABCD中,已知AB=2,M为BC的中点,若N为正方形内(含边界)任意一点,则

正确答案
6
解析
解析已在路上飞奔,马上就到!
知识点
12.函数



正确答案
8
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知函数


①函数

②函数

③若



④对任意


其中正确命题的序号是____________.(写出所有正确命题的编号)
正确答案
①③④
解析
解析已在路上飞奔,马上就到!
知识点
15. 在数列



(Ⅰ)证明:数列
(Ⅱ)求
(Ⅲ)求数列


正确答案
(Ⅰ) 
由定义知数列
(Ⅱ)因为数列
则
(Ⅲ) 
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知函数
(1)若函数 f(x)在点x=1处的切线与直线
(2)若f(x)在区间[0,1]上为单调减函数,求b的取值范围.
正确答案
(1)
因为与直线
又f(-1)=ln(2-1)-1-4+c=0,所以c=5 f(x)=ln(x+2)-x2+4x-5,

当
当
又f(0)=ln2+5,f(3)=ln5+8,所以f(x)在[0,3]最小值为ln2+5
(2)因为f(x)是减函数
所以
因为

所以当b≤-
解析
解析已在路上飞奔,马上就到!
知识点
19.设函数
(1)若在定义域内存在


(2)若函数


正确答案
(1)要使得不等式

求导得:
∵函数

当



当


∴



(2)由
由题设可得:方程

设

∵
从而有

画出函数





解析
解析已在路上飞奔,马上就到!
知识点
16.盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球.规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得
(I)求取出的3个球得分之和恰为1分的概率;
(II)设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知向量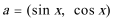
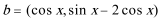
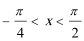
(Ⅰ)若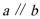

(Ⅱ)设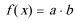
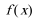
(Ⅲ)函数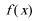
正确答案
(I)若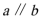
又∵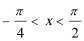

∴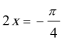
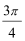
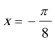
(II)
令
得,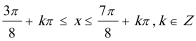
∴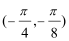

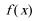
(Ⅲ)是,将函数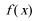
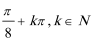
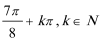
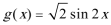

解析
解析已在路上飞奔,马上就到!
知识点
20. 已知




(1)记

(2)对






(3)求
正确答案
(1)证明:
令




(2)令




又


由①-②得
(3)

又

解析
解析已在路上飞奔,马上就到!