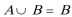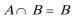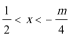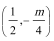- 真题试卷
- 模拟试卷
- 预测试卷
7.某班有50名学生,其中15人选修A课程,另外15人选修B课程,其它人不选任何课程,从中任选两名学生,则他们选修不同课程的学生概率为______。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 若函数


正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
2.方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.在等比数列


正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
4.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设





①函数

②函数

③函数
④函数
正确答案
①②③
解析
解析已在路上飞奔,马上就到!
知识点
9.若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.对于集合N={1, 2, 3,…, n}及其它的每一个非空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减、加后继的数。例如集合{1, 2, 4, 6, 9}的交替和是9–6+4–2+1=6,集合{5}的交替和为5。当集合N中的n=2时,集合N={1, 2}的所有非空子集为{1},{2},{1, 2},则它的“交替和”的总和S2=1+2+(2–1)=4,请你尝试对n=3、n=4的情况,计算它的“交替和”的总和S3、S4,并根据其结果猜测集合N={1, 2, 3,…, n}的每一个非空子集的“交替和”的总和Sn= _______。
正确答案
n∙2n–1
解析
解析已在路上飞奔,马上就到!
知识点
10.将正奇数按如下规律填在5列的数表中:则2007排在该表的第_____ 行,第_____ 列(行是从上往下数,列是从左往右数)
正确答案
第251行第5列
解析
解析已在路上飞奔,马上就到!
知识点
13.下列函数表示同一函数的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设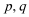
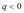
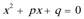
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.函数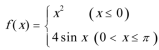
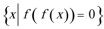
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.设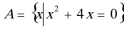
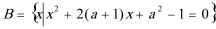
(1)若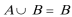
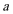
(2)若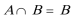
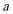
正确答案
(1)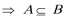
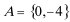
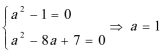
(2)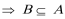
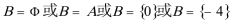
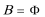
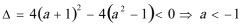
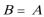
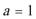
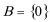
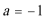
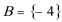
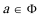
综上得 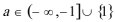
解析
解析已在路上飞奔,马上就到!
知识点
20.已知

(1)方程

(2)动点(x,y)在曲线
(3)由


正确答案
(1)
(2)根据



(3)不能,如再加条件

解析式
解析
解析已在路上飞奔,马上就到!
知识点
22.函数


(1)若函数

(2)求


(3)若函数


正确答案
(1) 

(2)
(3)
当

当

当

当

当

解析
解析已在路上飞奔,马上就到!
知识点
17.设O为坐标原点,已知向量






正确答案
由

又分母不为零,


解析
解析已在路上飞奔,马上就到!
知识点
18.设函数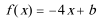
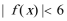
(1)求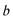
(2)解不等式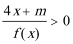
正确答案
(1)∵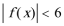
∴
(2)由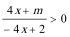
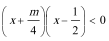
①当
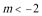
②当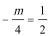
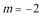
③当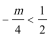
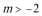
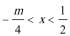
∴当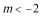
当
当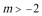

解析
解析已在路上飞奔,马上就到!
知识点
21.政府决定用“对社会的有效贡献率”对企业进行评价用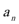
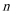
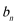

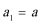
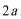
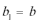
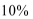

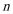
(1)求该企业第一年和第二年的“对社会的有效贡献率”;
(2)试问:从第几年起该企业“对社会的有效贡献率”不低于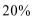
正确答案
(1)因为 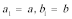
根据题意: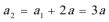

所以 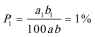

该企业第一年和第二年的“对社会的有效贡献率”分别为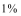
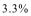
(2)因为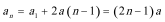
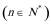
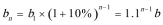
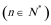
所以 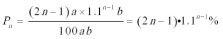
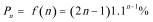
证法1: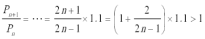
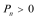
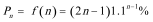
证法2: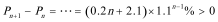

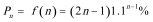
再验证: 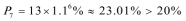
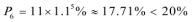
故,从第七年起该企业“对社会的有效贡献率”不低于
解析
解析已在路上飞奔,马上就到!