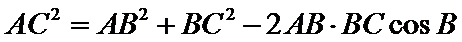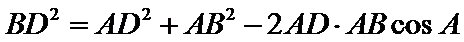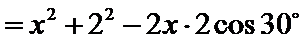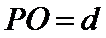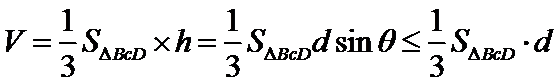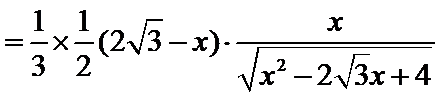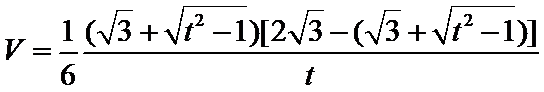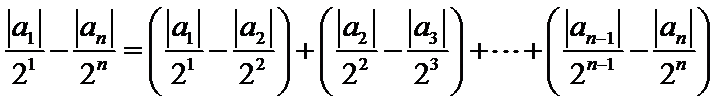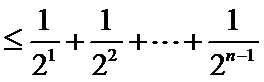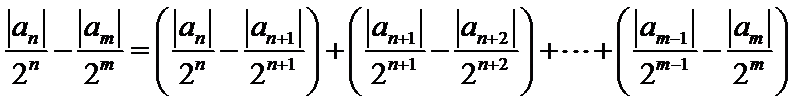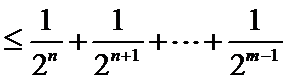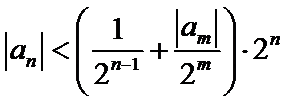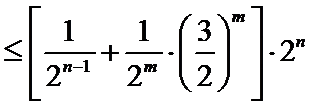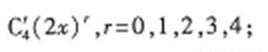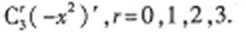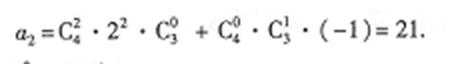- 真题试卷
- 模拟试卷
- 预测试卷
4.命题“

正确答案
解析






考查方向
解题思路
全称量词否定是特称量词,特称量词否定是全称量词
易错点
全称量词与特称量词复合命题的否定形式的不确定。
知识点
5.设函数

正确答案
解析
当




取




考查方向
解题思路
明显常数C不会对周期产生影响,只要判断
易错点
对函数最小正周期的理解偏差导致错误,可能会选C
知识点
6.如图,点列








正确答案
解析
.















考查方向
解题思路
直观判断,由于




易错点
没有发现点列
知识点
7.已知椭圆



正确答案
解析
.由题意知




考查方向
解题思路
根据焦点重合找出m,n的关系,

易错点
离心率之积的判断会出错。
知识点
2.已知互相垂直的平面

正确答案
解析
.由题意知



考查方向
解题思路
本题可以用排除法,依据题意与选项画出相应的图示,选项A,B,D可以举反例直接排除,为确保正确,再对选项C进行论证。
易错点
这样的题切忌逐个证明,应先排除几个。
知识点
8.已知实数
正确答案
解析
A.令


考查方向
解题思路
举反例排除法
易错点
逐个去证明,方法不可取。
知识点
1.已知集合P={x∈R︱1≤x≤3},Q={x∈R︱x²≥4},则P∪(CRQ)= ( )
正确答案
解析
根据补集的运算得
考查方向
解题思路
先求集合
易错点
补集端点的取舍
知识点
3.在平面上,过点P作直线l的垂线所得的垂足称为点P在直线l上的投影,由区域
正确答案
解析
.如图









考查方向
解题思路
先画出可行域,再画出直x+y-2=0,根据题意作出投影构成的线段,最后计算。
易错点
可行域中的点在直线的投影构成的线段的理解不到位。
知识点
9.若抛物线
正确答案
9
解析
.
考查方向
解题思路
将到焦点的距离转化到准线的距离
易错点
没有转化到准线的距离
知识点
10.已知
正确答案

解析
.
考查方向
解题思路
对
易错点
没有对
知识点
14.如图,在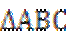
正确答案
解析
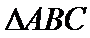
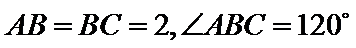
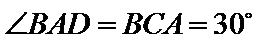
由余弦定理可得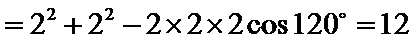
所以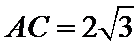
设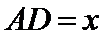
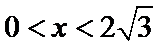
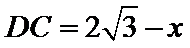
在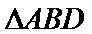
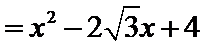
故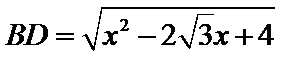
在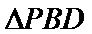
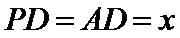
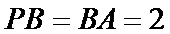
由余弦定理可得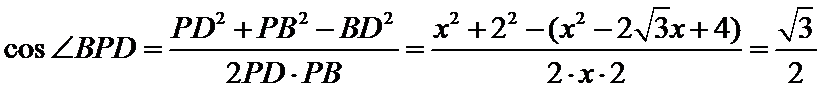
所以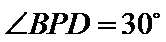
过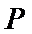
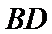
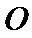
则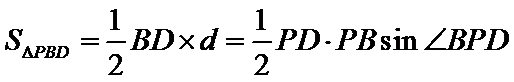
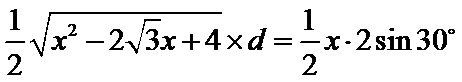
解得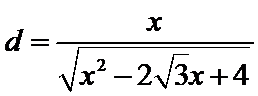
而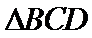
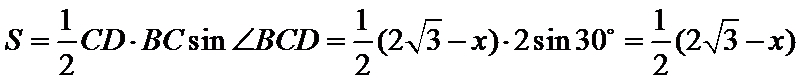
设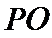
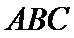
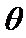
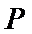
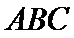
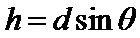
故四面体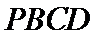
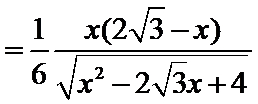
设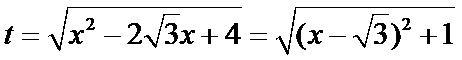
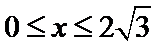
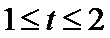
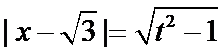
(2)当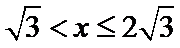
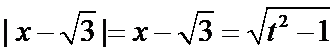
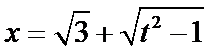
此时,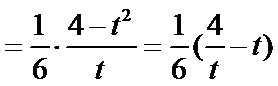
由(1)可知,函数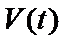
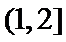
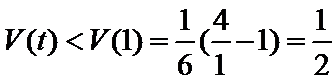
综上,四面体
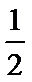
考查方向
解题思路
设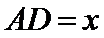
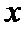
易错点
体积无法写成关于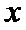
知识点
11.某几何体的三视图如图所示(单位:cm),则该几何体的表面积是 cm2,体积是 
正确答案
72;32
解析
.几何体为两个相同长方体组合,长方体的长宽高分别为4,2,2,所以体积为
考查方向
解题思路
根据三视图得知几何体为两个相同长方体组合,在进行计算。
易错点
空降想象力缺乏,不知道几何体的组成,还有重合部分的表面积没有减去。
知识点
12.已知

正确答案
4;2
解析
.设

因此
考查方向
解题思路
对


易错点
不知道

知识点
13.设数列




正确答案
1;121
解析
考查方向
解题思路
求


易错点
递推
知识点
15.已知向量a,b,|a|=1,|b|=2,若对任意单位向量e,均有|a·e|+|b·e|
正确答案
解析

考查方向
解题思路
利用极化不等式
易错点
对向量e任意性的理解。
知识点
如图,在三棱台





18.求证:
19.求二面角
正确答案
延长



因为平面





又因为






所以

解析
见答案。
考查方向
解题思路
先证


易错点
没有对面BCFE的分析,建立坐标系不当或对棱台上下底面比例性质不清楚,导致点坐标计算出错。
正确答案
解析
过点


因为





所以,

在



在



所以,二面角

考查方向
解题思路
先建立空间直角坐标系,再计算平面


易错点
没有对面BCFE的分析,建立坐标系不当或对棱台上下底面比例性质不清楚,导致点坐标计算出错。
设

20.求使得等式
21.(i)求
(ii)求

正确答案
[2,2a]
解析
由于
当

当

所以,使得等式


考查方向
解题思路
分别对




易错点
对函数
正确答案

解析
(i)设函数



所以,由


(ii)当

当

所以,
考查方向
解题思路
(i)先求函数










易错点
对函数
设数列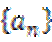
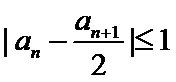
24.求证:
25.若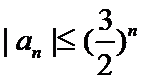
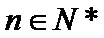
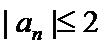
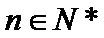
正确答案
由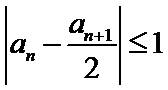
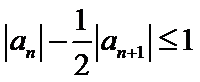
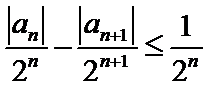
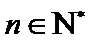
所以
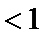
因此
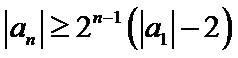
解析
见答案
考查方向
解题思路
先利用三角形不等式得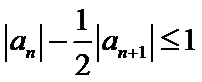
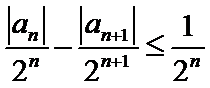
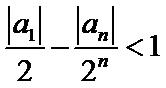
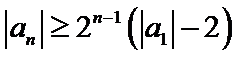
正确答案
任取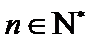
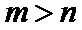
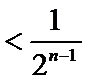
故
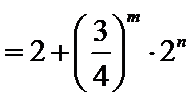
从而对于任意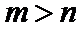
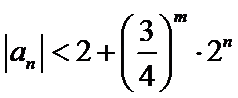
由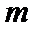
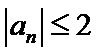
否则,存在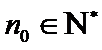
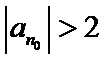
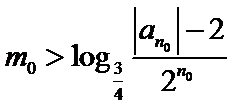
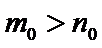
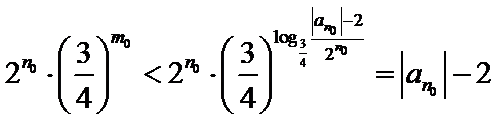
与①式矛盾.
综上,对于任意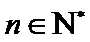
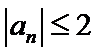
解析
见答案
考查方向
解题思路
由(I)可得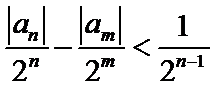
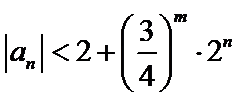
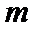
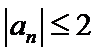
在

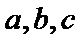
16.证明:
17.若

正确答案
由正弦定理得
故
于是
又




因此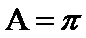

所以,
解析
见答案
考查方向
解题思路
先利用三角形正弦定理进行边角互化,再将角C用A,B表示,化简即可以得到结论
易错点
两正弦相等可能会缺少两角互补的情况
正确答案

解析
由
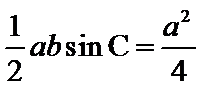

因




当



综上,

考查方向
解题思路
选择恰当的面积公式,进行边角互化。
易错点
两正弦相等可能会缺少两角互补的情况
如图,设椭圆C:
22.求直线
23.若任意以点
正确答案
解析
联立方程
解之得

解题思路
本小题考察直线和椭圆相交的弦长问题,比较简单,属于送分性质,同时也可以为第23小题的解答坐铺垫。
易错点
不会对条件“任意以点
正确答案
解析
假设圆与椭圆的公共点有



记直线





由(1)知
故
所以
由于
因此
对于上式关于

因此,任意以

离心率
解题思路
由于圆与椭圆至多有三个公共点,由于图形的对称性,圆与椭圆y轴单侧不可嫩有2个公共点,即弦长在y轴单侧处处不相等。
易错点
不会对条件“任意以点
自选模块数学试题
“复数与导数”模块(10分)
26.已知i为虚数单位,若复数z满足(z+i)2=2i,求复数z
27.求曲线y=2x2+lnx在点(1,2)处得切线方程。
正确答案
设复数z=a+bi,a,b∈ R,由题意得
a2—(b十1)2十2a(b十1)i=2i,
解得
正确答案
由于
“计数原理与概率”模块(10分)
28.已知(1+2x)4(1-x2)3=a0+a1x+a2x2+…a10x10,求a2的值
29.设袋中共有8个球,其中3个白球、5个红球,从袋中随机取出3个球,求至少有1个白球的概率
正确答案
因为( 1+2x)4二项展开式的通项为
( 1一x2 )3二项展开式的通项为
所以
正确答案
从袋中取出3个球,总的取法有 C83=56种;
其中都是红球的取法有 C53 = 10种.
因此,从袋中取出3个球至少有1个白球的概率是