- 真题试卷
- 模拟试卷
- 预测试卷
1.设集合A={(x,y)|x+y=1},B={(x,y)|x-2y=3},则满足M⊆(A∩B)的集合M的个数是( )
正确答案
解析
由题中集合可知,集合A表示直线x+y=1上的点,集合B表示直线x-2y=3上的点,联立
知识点
4.程序框图如下图所示,当

正确答案
解析
略。
知识点
5.设集合M={x|0<x≤3},N={x|0<x≤2},那么“a∈M”是“a∈N”的( )
正确答案
解析
略。
知识点
6.设实数x,y满足不等式组
正确答案
解析
如图所示,不等式组表示的平面区域是△ABC的内部(含边界),x2+y2表示的是此区域内的点(x,y)到原点距离的平方.从图中可知最短距离为原点到直线BC的距离,其值为1;最远的距离为AO,其值为2,故x2+y2的取值范围是[1,4].
知识点
7.一个几何体的三视图如图所示,其中俯视图是菱形,则该几何体的侧面积为( )
正确答案
解析
由三视图还原为空间几何体,如图所示,则有OA=OB=1,
又PB⊥平面ABCD,
∴PB⊥BD,PB⊥AB,
∴PD=


从而有PA2+DA2=PD2,∴PA⊥DA,
∴该几何体的侧面积
知识点
8.定义区间(a,b),[a,b),(a,b],[a,b]的长度均为d=b-a,多个区间并集的长度为各区间长度之和,例如,(1,2)∪[3,5)的长度d=(2-1)+(5-3)=3.用[x]表示不超过x的最大整数,记{x}=x-[x],其中x∈R.设f(x)=[x]·{x},g(x)=x-1,当0≤x≤k时,不等式f(x)<g(x)的解集区间的长度为5,则k=( )
正确答案
解析
f(x)=[x]·{x}=[x]·(x-[x])=[x]x-[x]2,由f(x)<g(x),得[x]x-[x]2<x-1,即
知识点
3.曲线
正确答案
解析
当





当





知识点
2.下列函数中,既是偶函数又在(-∞,0)上单调递增的是( )
正确答案
解析
选C 函数y=x2在(-∞,0)上是减函数;函数y=2|x|在(-∞,0)上是减函数;函数y=
知识点
11.直线x-2y+2=0过椭圆
正确答案

解析
直线x-2y+2=0与x轴的交点为(-2,0),即为椭圆的左焦点,故c=2.
直线x-2y+2=0与y轴的交点为(0,1),即为椭圆的顶点,故b=1.
故a2=b2+c2=5,椭圆方程为
知识点
10.已知点M(5,-6)和向量a=(1,-2),若
正确答案
(2,0)
解析

设N(x,y),则
所以
知识点
12.在等差数列{an}中,a1=7,公差为d,前 n项和为Sn ,当且仅当n=8 时Sn 取得最大值,则d 的取值范围为________.
正确答案
解析
由题意,当且仅当n=8时Sn有最大值,可得



知识点
14.已知函数f(x)=

正确答案
解析
f(x)=3sin



∵x∈



∴-
知识点
9.已知



正确答案
解析


知识点
13.从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同的工作,若其中甲、乙两名志愿者不能从事翻译工作,则选派方案共有________.
正确答案
240种
解析
根据题意,由排列可得,从6名志愿者中选出4人分别从事四项不同工作,有A=360种不同的情况,其中包含甲从事翻译工作,有A=60种,乙从事翻译工作,有A=60种,若其中甲、乙两名志愿者都不能从事翻译工作,则选派方案共有360-60-60=240种.
知识点
15.(本小题满分13分)已知向量
(1)求
(2)在




正确答案
见解析。
解析
(1)
(2)根据正弦定理知:
∵






知识点
20.设函数F(x)在区间D上的导函数为F1(x),F1(x)在区间D上的导函数为F2(x),如果当x∈D时,F2(x)≥0,则称F(x)在区间D上是下凸函数.已知e是自然对数的底数,f(x)=ex-ax3+3x-6.
(1)若f(x)在[0,+∞)上是下凸函数,求a的取值范围;
(2)设M(x)=f(x)+f(-x)+12,n是正整数,求证:M(1)M(2)…M(n)>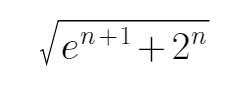
正确答案
见解析。
解析
(1)f′(x)=ex-3ax2+3,设F1(x)=f′(x),则F1′(x)=ex-6ax.
∵f(x)在[0,+∞)上是下凸函数,
∴当x∈[0,+∞)时,F1′(x)=ex-6ax≥0.
当x=0时,1≥0成立,即F1′(x)=ex-6ax≥0成立,此时a∈R.
当x∈(0,+∞)时,由F1′(x)=ex-6ax≥0得,
设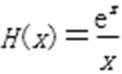
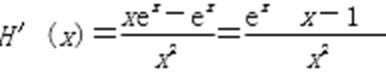
∴当x∈(1,+∞)时,H′(x)>0,H(x)单调递增;
当x∈(0,1)时,H′(x)<0,H(x)单调递减,
∴当x=1时,H(x)取得最小值H(1)=e,
∴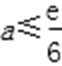
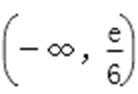
(2)∵f(x)=ex-ax3+3x-6,
∴M(x)=f(x)+f(-x)+12=ex+e-x>0.
∵M(x1)M(x2)=ex1+x2+ex1-x2+ex2-x1+e-x1-x2>ex1+x2+ex1-x2+ex2-x1,
又ex1-x2+ex2-x1≥
∴M(1)M(n)>en+1+2,M(2)M(n-1)>en+1+2,
M(3)M(n-2)>en+1+2,…,M(n)M(1)>en+1+2,
∴[M(1)M(n)][M(2)M(n-1)]· …·[M(n)M(1)]>(en+1+2)n,
∴M(1)M(2)· …·
知识点
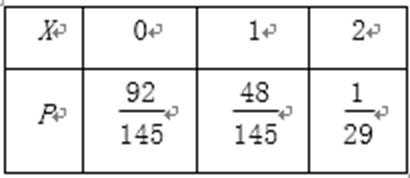
16.(本小题满分13分)某学校的三个学生社团的人数分布如下表(每名学生只能参加一个社团):
学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从三个社团成员中抽取18人,结果拳击社被抽出了6人.
(1)求拳击社团被抽出的6人中有5人是男生的概率;
(2)设拳击社团有X名女生被抽出,求X的分布列.
正确答案
见解析。
解析
(1)由于按分层抽样的方法从三个社团成员中抽取18人,拳击社被抽出了6人,
∴
∴m=2.
设A为“拳击社团被抽出的6人中有5人是男生”,
则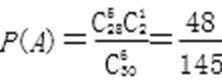
(2)由题意可知:X=0,1,2,

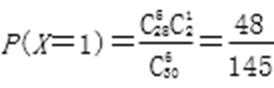

X的分布列为
知识点
17.(本小题满分13分)如图,在四棱锥PABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=
(1)求证:EF∥平面PAD;
(2)求证:平面PAB⊥平面PDC;
(3)在线段AB上是否存在点G,使得二面角CPDG的余弦值为
正确答案
见解析。
解析
(1)
如图,连接AC,交BD于点F,底面ABCD为正方形,
F为AC中点,E为PC中点.
所以在△CPA中,EF∥PA.
又PA⊂平面PAD,EF⊄平面PAD,
所以EF∥平面PAD.
(2)证明:因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD.
底面ABCD为正方形,CD⊥AD,CD⊂平面ABCD,所以CD⊥平面PAD.
又PA⊂平面PAD,所以CD⊥PA.
又PA=PD=

又CD∩PD=D,且CD,PD⊂平面PDC,所以PA⊥平面PDC.
又PA⊂平面PAB,所以平面PAB⊥平面PDC.
(3)如图,取AD的中点O,连接OP,OF,因为PA=PD,所以PO⊥AD.
又侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,所以PO⊥平面ABCD,
而O,F分别为AD,BD的中点,所以OF∥AB,
又底面ABCD是正方形,故OF⊥AD,
以O为原点,建立空间直角坐标系Oxyz如图所示,则有A(1,0,0),C(-1,2,0),F(0,1,0),D(-1,0,0),P(0,0,1),若在AB上存在点G,使得二面角CPDG的余弦值为
则


设平面PGD的法向量为n=(x,y,z).
则
即
令y=-2,得n=(a,-2,-a),
所以
解得
所以,在线段AB上存在点

知识点
18.(本小题满分13分)已知函数f(x)=ln x,
(1)若f(x)与g(x)在x=1处相切,求g(x)的表达式;
(2)若φ(x)=
正确答案
见解析。
解析
(1)由已知得f′(x)=

又∵g(1)=0=
(2)∵φ(x)=

∴φ′(x)=
即x2-(2m-2)x+1≥0在[1,+∞)上恒成立,
则2m-2≤x+
∵x+
故数m的取值范围是(-∞,2].
知识点
19.(本小题满分14分)(2015·衡水中学二调)已知椭圆C的对称中心为原点O,焦点在x轴上,左、右焦点分别为F1和F2,且|F1F2|=2,点
(1)求椭圆C的方程;
(2)过F1的直线l与椭圆C相交于A,B两点,若△AF2B的面积为
正确答案
见解析。
解析
(1)由题意知c=1, 
a=2,故椭圆C的方程为
(2)①当直线l⊥x轴时,可取
②当直线l与x轴不垂直时,设直线l的方程为y=k(x+1),代入椭圆方程得(3+4k2)x2+8k2x+4k2-12=0,
显然Δ>0成立,设A(x1,y1),B(x2,y2),
则x1+x2=-

可得
又圆F2的半径
∴△AF2B的面积为
代简得:17k4+k2-18=0,得k=±1,
∴r=