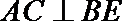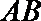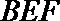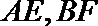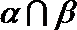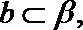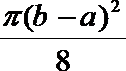- 真题试卷
- 模拟试卷
- 预测试卷
3.已知:a>0,b>0且a+b=1,则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知等差数列{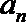
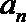
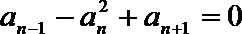
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.一个几何体的三视图如图1所示,已知这个几何体的体积为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.如图,正方体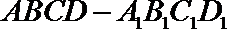
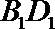
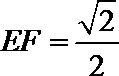
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设实数集R上定义的函数y=f(x),对任意的x
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知平面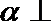
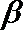
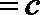

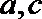
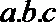
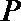
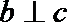
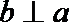
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
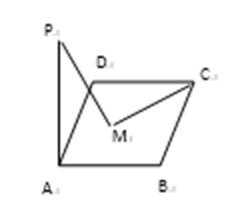
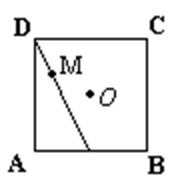
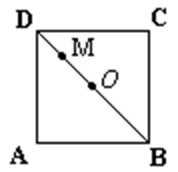
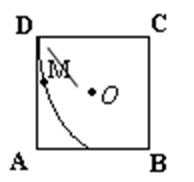
11.如图△ADP为正三角形,四边形ABCD为正方形,平面PAD⊥平面ABCD,M为平面ABCD内的一动点,且满足MP=MC.则点M在正方形ABCD内的轨迹为(O为正方形ABCD的中心)( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知ABCD-A1B1C1D1为单位正方体,黑白两个蚂蚁从点A出发沿棱向前爬行,每走完一条棱称为“走完一段”,白蚂蚁爬行的路线是AA1→A1D1→……,黑蚂蚁爬行的路线是AB→BB1→……,它们都遵循如下规则:所爬行的第


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设等差数列









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.若直线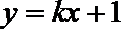
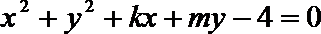
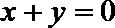
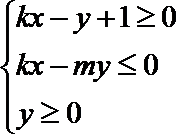
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
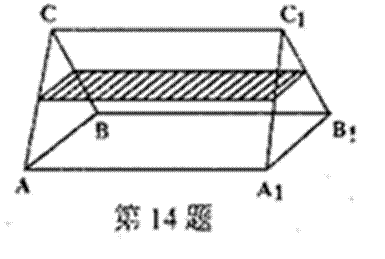
14.一个三棱柱容器中盛有水,侧棱AA1=8,如图当侧面AA1B1B水平放置时,液面恰好过AC、BC、A1C1的中点,如果当底面ABC水平放置时,液面的高是__________.
正确答案
6
解析
解析已在路上飞奔,马上就到!
知识点
16.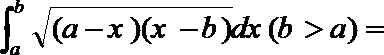
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 在直三棱柱



(1)求证:MN∥平面
(2)求点
(3)求二面角
正确答案
(1)如图所示,取B1C1中点D,连结ND、A1D
∴DN∥BB1∥AA1
又DN=
∴四边形A1MND为平行四边形。
∴MN∥A1 D 又 MN 

∴MN∥平面
(2)因三棱柱
∴C1 C ⊥BC,又∠ACB=90°∴BC⊥平面A1MC1
在平面ACC1 A1中,过C1作C1H⊥CM,又BC⊥C1H,故C1H为C1点到平面BMC的距离。
在等腰三角形CMC1中,C1 C=2
∴
(3)在平面ACC1A1上作CE⊥C1M交C1M于点E,A1C1于点F,则CE为BE在平面ACC1A1上的射影,
∴BE⊥C1M, ∴∠BEF为二面角B-C1M-A的平面角,
在等腰三角形CMC1中,CE=C1H=
∴∠BEC=arctan

即二面角


解析
解析已在路上飞奔,马上就到!
知识点
19.如图,已知平行四边形





(Ⅰ)求证:
(Ⅱ)当四棱锥


正确答案
(Ⅰ)证法1:∵


∴四边形EFBC是平行四边形 ∴H为FC的中点
又∵G是FD的中点
∴
∵

∴GH∥平面CDE
证法2:连结EA,∵ADEF是正方形 ∴G是AE的中点
∴在⊿EAB中,
又∵AB∥CD,∴GH∥CD,
∵

∴GH∥平面CDE
(Ⅱ)∵平面ADEF⊥平面ABCD,交线为AD且FA⊥AD,
∴FA⊥平面ABCD.
∵BD⊥CD, 

∴FA=2,

∴ 
∴

要使



∵



解法1:在平面DBC内过点D作
∵

∴
∵当

∴
∴
即平面ECF与平面ABCD所成的二面角的余弦值为
解法2:以点D为坐标原点,DC所在的直线为




则
∴

设平面ECF与平面ABCD所成的二面角为
平面ECF的法向量
由
令
又∵平面ABCD的法向量为
∴即平面ECF与平面ABCD所成的二面角的余弦值为
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(Ⅰ)讨论函数
(Ⅱ)设函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图:在山脚A测得山顶P的仰角为


求山高h(单位:米)
正确答案
在三角形ABC中
解析
解析已在路上飞奔,马上就到!
知识点
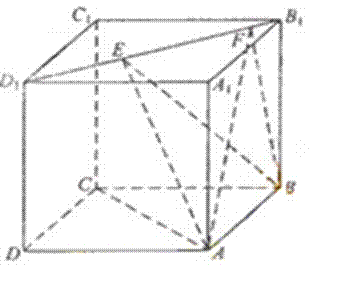
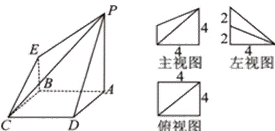
20.下图是一几何体的直观图、主视图、俯视图、左视图.
(Ⅰ)若
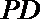
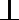
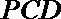
(Ⅱ)证明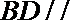
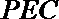
(Ⅲ)求面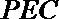
正确答案
(Ⅰ)由几何体的三视图可知,底面ABCD是边长为4的正方形,PA⊥面ABCD,
PA∥EB,PA=2EB=4.∵PA=AD,F为PD的中点,
∴PD⊥AF,
又∵CD⊥DA,CD⊥PA,PA∩DA=A,
∴CD⊥面ADP,
∴CD⊥AF.又CD∩DP=D, ∴AF⊥面PCD.
(Ⅱ)取PC的中点M,AC与BD的交点为N,连结MN,
∴MN=
∴MN=EB,MN∥EB,故四边形BEMN为平行四边形,
∴EM∥BN,又EM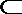
(Ⅲ)分别以BC,BA,BE为x,y,z轴建立空间直角坐标系,
则C( 4,0,0),D(4 ,4 , 0),E(0,0,2),A(0,4 ,0),P(0,4,4),
∵F为PD的中点,∴F(2,4,2).
∵AF⊥面PCD,∴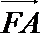
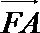
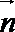
则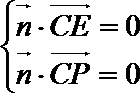
∴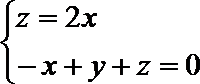
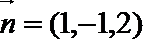
∴
∴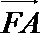
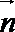
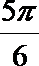
面PEC与面PDC所成的二面角(锐角)的余弦值为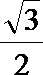
解析
解析已在路上飞奔,马上就到!
知识点
21.设
(1)求实数a;
(2)求数列{xn}的通项公式;
(3)若
正确答案
(1)由
解析
解析已在路上飞奔,马上就到!