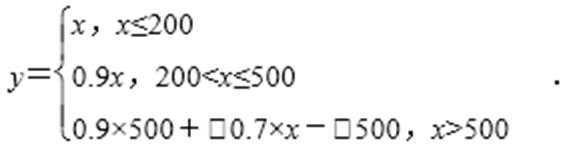- 真题试卷
- 模拟试卷
- 预测试卷
6．如果执行下边的程序框图，输入正整数N（N≥2）和实数a1、a2、…、aN，输出A、B，则（ ）
AA+B为a1，a2，…，aN的和
B
CA和B分别是a1，a2，…，aN中最大的数和最小的数
DA和B分别是a1，a2，…，aN中最小的数和最大的数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．任何一个算法都必须有的基本结构是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．下图是计算某年级500名学生期末考试（满分为100分）及格率q的程序框图，则图中空白框内应填入（ ）
Aq=
Bq=
Cq=
Dq=
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2．下列说法正确的是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．画流程图的一般要求为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．下图是用模拟方法估计圆周率
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
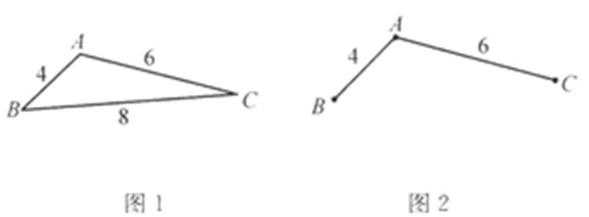
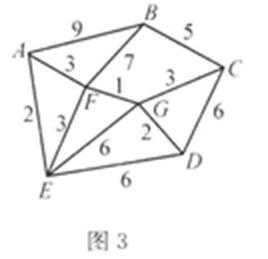
8．某地区规划道路建设，考虑道路铺设方案，方案设计图中，求表示城市，两点之间连线表示两城市间可铺设道路，连线上数据表示两城市间铺设道路的费用，要求从任一城市都能到达其余各城市，并且铺设道路的总费用最小。例如：在三个城市道路设计中，若城市间可铺设道路的线路图如图1，则最优设计方案如图2，此时铺设道路的最小总费用为10。
现给出该地区可铺设道路的线路图如图3，则铺设道路的最小总费用为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．有一堆形状、大小相同的珠子，其中只有一粒重量比其它的轻，某同学经过思考，他说根据科学的算法，利用天平，三次肯定能找到这粒最轻的珠子，则这堆珠子最多有几粒（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．为确保信息安全，信息需加密传输，发送方由明文→密文（加密），接收方由密文→明文（解密），已知加密规则为：明文a，b，c，d对应密文a+2b，2b+c，2c+3d，4d，例如，明文1，2，3，4对应密文5，7，18，16．当接收方收到密文14，9，23，28时，则解密得到的明文为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1．下列语句中是算法的个数为（ ）
①从济南到巴黎：先从济南坐火车到北京，再坐飞机到巴黎；
②统筹法中“烧水泡茶”的故事；
③测量某棵树的高度，判断其是否是大树；
④已知三角形的一部分边长和角，借助正余弦定理求得剩余的边角，再利用三角形的面积公式求出该三角形的面积。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．给出以下四个问题，
①输入一个数x，输出它的相反数；
②求面积为6的正方形的周长；
③求三个数a，b，c中的最大数；
④求二进数111111的值。
其中不需要用条件语句来描述其算法的有（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．284和1024的最小公倍数是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14．有如下程序框图（如下图所示），则该程序框图表示的算法的功能是____________。
正确答案
计算并输出使1×3×5×7…× >10 000成立的最小整数
解析
解析已在路上飞奔，马上就到！
知识点
13．阅读下图所示的程序框图，运行相应地程序，输出的s值等于____________。
正确答案
-3
解析
解析已在路上飞奔，马上就到！
知识点
15．阅读如图所示的程序框图，运行相应的程序，输出的结果
正确答案
9
解析
解析已在路上飞奔，马上就到！
知识点
16．将“杨辉三角”中的数从左到右、从上到下排 成一数列：1，1，1，1，2，1，1，3，3，1，1，4，6，4，1，…， 下图所示程序框图用来输出此数列的前若干项并求其和，若输入m=4则相应最后的输出S的值是__________
正确答案
2
解析
解析已在路上飞奔，马上就到！
知识点
17．以下是求函数y=|x+1|+|x-2|的值的流程图。回答以下问题：
（1） ①处应填入的内容是_______;
②处应填入的条件是_______;
③处应填入的内容是_______.
（2） 若输出的y的值大于7，求输入的x的值的范围
正确答案
（1）
（2）当x<-1时，由y>7得x<-3，
当x>2时，由y>7得x>4，
所以，输入的x的值的范围是x<-3或x>4
解析
解析已在路上飞奔，马上就到！
知识点
18．设计算法求
正确答案
这是一个累加求和问题，共99项相加，可设计一个计数变量，一个累加变量，用循环结构实现这一算法．程序框图如下图所示：
解析
解析已在路上飞奔，马上就到！
知识点
19．编写一个程序，求1!+2!+…+10!的值。
正确答案
程序为：
s=0
i=1
j=1
WHILE i<=10
j=j*i
s=s+j
i=i+1
WEND
PRINT s
END
解析
解析已在路上飞奔，马上就到！
知识点
20．国庆期间，某超市对顾客实行购物优惠活动，规定一次购物付款总额：
①若不超过200元，则不予优惠；
②若超过200元，但不超过500元，则按标价价格给予9折折惠；
③如果超过500元，500元的部分按②条优惠，超过500元的部分给予7折优惠，
设计一个收款的算法，并画出程序框图。
正确答案
依题意，付款总额y与标价x之间的关系式为（单位为元）
算法分析：
第一步：输入x值；
第二步：判断，如果x≤200，则输出x，结束算法；否则执行第三步；
第三步：判断，如果x≤500成立，则计算y＝0．9×x，并输出y，结束算法；否则执行第四步；
第四步：计算：y＝0．9×500＋0．7×（x－500），并输出y，结束算法．
程序框图：
解析
解析已在路上飞奔，马上就到！
知识点
21．中国网通规定：拨打市内电话时，如果不超过3分钟，则收取话费0．22元；如果通话时间超过3分钟，则超出部分按每分钟0．1元收取通话费，不足一分钟按以一分钟计算。设通话时间为t（分钟），通话费用y（元），如何设计一个程序，计算通话的费用。
正确答案
算法分析：
数学模型实际上为：y关于t的分段函数。
关系是如下：
其中[t－3]表示取不大于t－3的整数部分。
算法步骤如下：
第一步：输入通话时间t；
第二步：如果t≤3，那么y = 0．22；否则判断t∈Z 是否成立，若成立执行y= 0．2+0．1× （t－3）；否则执行y = 0．2+0．1×（ [t－3]+1）。
第三步：输出通话费用c 。
算法程序如下：
INPUT “请输入通话时间：”；t
IF t<=3 THEN
y=0．22
ELSE
IF INT（t）=t THEN
y=0．22+0．1*（t－3）
ELSE
y=0．22+0．1*（INT（t－3）+1）
END IF
END IF
PRINT “通话费用为：”；y
END
解析
解析已在路上飞奔，马上就到！
知识点
22．已知数列
（1）分别写出当
（2）当输入
（3）在（2）的条件下，若令
正确答案
（1）当
当
（2）
（3）
解析
解析已在路上飞奔，马上就到！