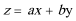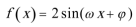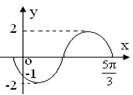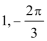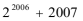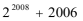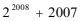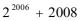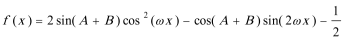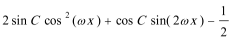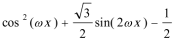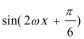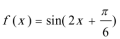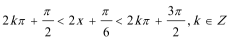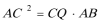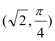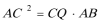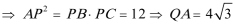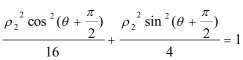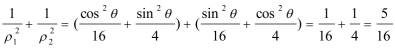- 真题试卷
- 模拟试卷
- 预测试卷
1.设全集为实数集R,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居众显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
①平均数
②标准差
③平均数

④平均数
⑤众数等于1且极差小于或等于1。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知三棱锥的三视图如图所示,则它的外接球表面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知圆的方程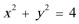
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设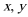
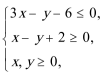
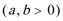
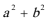
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数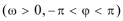
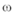
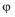
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 双曲线








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.在长方体ABCD—A1B1C1D1中,对角线B1D与平面A1BC1相交于点E,则点E为△A1BC1的( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 设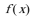
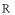

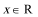

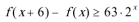

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 在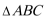

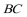
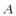
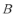
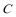
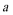
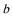
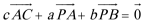
正确答案
等边三角形
解析
解析已在路上飞奔,马上就到!
知识点
14.某程序框图如图所示,该程序运行后输出的
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在






正确答案
2005
解析
解析已在路上飞奔,马上就到!
知识点
13.在区间[-6,6],内任取一个元素xO ,若抛物线y=x2在x=xo处的切线的倾角为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在△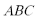
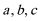
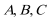
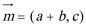
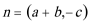
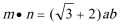
(1)求角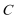
(2)函数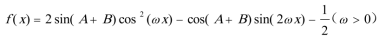
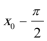
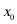
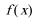
正确答案
(1)因为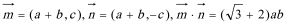
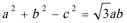
故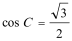
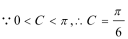
(2)
=
=
=
因为相邻两个极值的横坐标分别为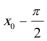
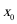
所以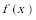
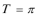
所以
由
所以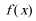
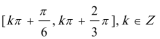
解析
解析已在路上飞奔,马上就到!
知识点
19.现有4个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择,为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(1)求这4个人中恰有2人去参加甲游戏的概率;
(2)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;
(3)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记ξ=|X-Y|,求随机变量ξ的分布列与数学期望Eξ。
正确答案
依题意,这4个人中,每个人去参加甲游戏的概率为,去参加乙游戏的概率为.设“这4个人中恰有i人去参加甲游戏”为事件
(1)这4个人中恰有2人去参加甲游戏的概率
(2)设“这4个人中去参加甲游戏的人数大于去参加乙游戏的人数”为事件B,则
由于

所以,这4个人去参加甲游戏的人数大于去参加乙游戏的人数的概率为.
(3)ξ的所有可能取值为0,2,4. 由于





所以ξ的分布列是
随机变量ξ的数学期望
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆





(Ⅰ)求椭圆
(Ⅱ)若动点









正确答案
(Ⅰ)因为点

所以

因为椭圆

所以

解得


(Ⅱ)设

①当直线




由

所以
因为

所以

所以
因为直线

所以直线

即


②当直线


此时直线


综上所述直线

解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数




(1)求
(2)设



(3)是否存在实数a,使得当

正确答案
(1)设




故函数
(2)证明:当


因为






又因为



所以当

(3)解:假设存在实数


则
(ⅰ)当





(ⅱ)当





(ⅲ)当






(ⅳ)当






所以
综上可知,存在实数


解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
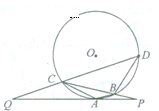
22.选修4—1:几何证明选讲
已知PQ与圆O相切于点A,直线PBC交圆于B、C两点,D是圆上一点,且AB∥CD,DC的延长线交PQ于点Q
(1) 求证:
(2) 若AQ=2AP,AB=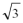
23.选修4—4:坐标系与参数方程
在平面直角坐标系中,曲线C1的参数方程为 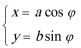
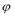
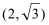
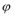
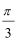
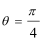
(1)求曲线C1,C2的方程;
(2)A(ρ1,θ),Β(ρ2,θ+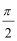
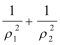
24. 选修4—5:不等式选讲
已知关于x的不等式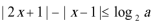
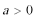
(1)当
(2)若不等式有解,求实数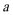
正确答案
22.(1)因为AB∥CD,所以∠PAB=∠AQC,
又PQ与圆O相切于点A,所以∠PAB=∠ACB,
因为AQ为切线,所以∠QAC=∠CBA,
所以△ACB∽△CQA,所以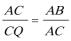
所以
(2)因为AB∥CD,AQ=2AP,
所以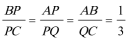
由AB=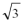
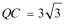
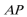
又因为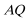
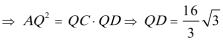
23.解:(1)将M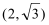
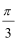
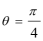
代入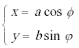
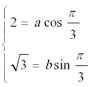
所以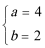

设圆C2的半径R,则圆C2的方程为:ρ=2Rcosθ(或(x-R)2+y2=R2),
∴R=1 ∴圆C2的方程为:ρ=2cosθ(或(x-1)2+y2=1)
(2)曲线C1的极坐标方程为: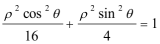
将A(ρ1,θ),Β(ρ2,θ+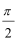
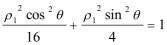
所以
即
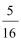
24.解:(1)当a=4时,不等式即|2x+1|-|x-1|≤2,
当x<−
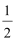
当−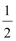

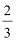
当x>1时,不等式为x+2≤2,此时x不存在.
综上,不等式的解集为{x|−4≤x≤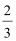
(2)设f(x)=|2x+1|-|x-1|=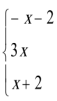
故f(x)的最小值为−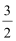
所以,当f(x)≤log2a有解,则有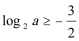
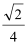
即a的取值范围是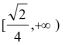
解析
解析已在路上飞奔,马上就到!
知识点
18.已知四边形ABCD满足


(1)求四棱锥
(2)证明:
(3)求面
正确答案
(1)取AE的中点M,连结B1M,
因为BA=AD=DC=
则B1M=
所以B1M⊥面AECD,
所以
(2)连结ED交AC于O,连结OF,因为AECD为菱形,OE=OD所以FO∥B1E,
所以
(3)连结MD,则∠AMD=




所以,


设面ECB1的法向量为

令x=1, 


故面

解析
解析已在路上飞奔,马上就到!