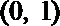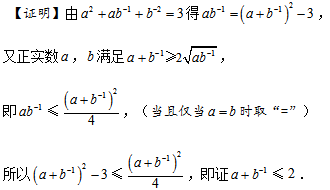- 真题试卷
- 模拟试卷
- 预测试卷
3. 命题:“

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 如图,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. “


正确答案
充分不必要
解析
解析已在路上飞奔,马上就到!
知识点
2. 已知复数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 设定义在区间




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 已知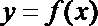
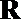
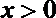
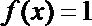
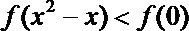
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 已知数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 若集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.记






可以推测,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.如图,三次函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知偶函数








正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知中心为







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.平面直角坐标系


(1)求

(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设定义在


(1)若


(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在△ABC中,角A,B,C的对边分别是a,b,c,且
(1)求
(2)试判断△ABC的形状,并说明理由。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,某兴趣小组测得菱形养殖区






(1)如图甲,养殖区在投食点

(2)如图乙,养殖区在投食点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.【选做题】
在A、B、C、D四小题中只能选做两小题。解答时应写出文字说明、证明过程或演算步骤。
A.几何证明选讲
如图,从圆O外一点P作圆O的两条切线,切点分别为A,B,AB与OP交于点M,设CD为过点M且不过圆O的一条弦,求证:O、C、P、D四点共圆。
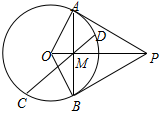
B.矩阵与变换
设矩阵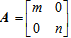
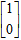
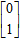
C.极坐标与参数方程
在极坐标系中,已知点O(0,0),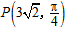
D.不等式选讲
设正实数a,b满足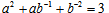
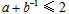
正确答案
A.
B.
C.
D.
解析
解析已在路上飞奔,马上就到!
知识点
20.设




(1)若
(2)试确定所有的自然数k,使得数列{an}能成等差数列。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.若函数









(1)已知


(2)试探究是否存在实数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.设

① 

②对任意的

(1)记




(2)记




正确答案
解析
解析已在路上飞奔,马上就到!