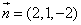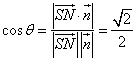理科数学静安区2014年高三试卷

精品

填空题
单选题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、填空题

2、单选题

3、简答题

真题试卷
模拟试卷
预测试卷

填空题本大题共14小题，每小题4分，共56分。把答案填写在题中横线上。

题型：填空题

分值: 4分

1．全集，集合，则（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

补集及其运算

题型：填空题

分值: 4分

7．已知函数有反函数，若，则=（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 4分

9．在极坐标系中，直线与直线的夹角大小为（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

题型：填空题

分值: 4分

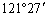
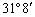
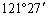
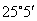
6．已知地球半径约为6371千米．上海的位置约为东经，北纬，台北的位置约为东经，北纬，则这两个城市之间的球面距离约为（）千米（结果保留到1千米）．

正确答案

673

解析

解析已在路上飞奔，马上就到！

知识点

球面距离及相关计算

题型：填空题

分值: 4分

10．如果随机变量的概率分布律由下表给出：则= （）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

定积分

题型：填空题

分值: 4分

13．已知是双曲线右支上的一点，、分别是圆和上的点，则的最大值等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：填空题

分值: 4分

14．已知集合，对于它的非空子集，将中每个元素都乘以后再求和，称为的非常元素和，比如的非常元素和为．那么集合的所有非空子集的非常元素和的总和等于（）．

正确答案

2560

解析

解析已在路上飞奔，马上就到！

知识点

轨迹方程

题型：填空题

分值: 4分

5．二项式展开式的前三项的系数成等差数列，则（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的性质及应用求二项展开式的指定项或指定项的系数

题型：填空题

分值: 4分

12．在由数字0、1、2、3、4、5所组成的没有重复数字的四位数中任取一个数，该数能被5 整除的概率是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域

题型：填空题

分值: 4分

11．已知虚数、满足和（其中），若，则（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复数代数形式的混合运算复数求模

题型：填空题

分值: 4分

2．已知，且为第二象限角，则的值为（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

同角三角函数间的基本关系三角函数的化简求值

题型：填空题

分值: 4分

3．若极限，则实数（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

数列的极限

题型：填空题

分值: 4分

4．已知，，，则（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

向量的模平面向量数量积的运算

题型：填空题

分值: 4分

8．将一个总体分为、、三层，其个体数之比为。若用分层抽样方法抽取容量为100的样本，则应从中抽取（）个个体

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

分层抽样方法

单选题本大题共4小题，每小题5分，共20分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

15．“”是“”的（）

A充分非必要条件

B必要非充分条件

C充要条件

D既非充分又非必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两圆的公切线条数及方程的确定

题型：单选题

分值: 5分

16．若，则一定是（）

A等腰三角形

B直角三角形

C锐角三角形

D钝角三角形

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

分值: 5分

17．函数的图像大致为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

知图选式与知式选图

题型：单选题

分值: 5分

18．正方体的棱长为2，动点、在棱上。动点、分别在棱、上，若，，， (大于零)，则四面体的体积（）

A与都有关

B与有关，与无关

C与有关，与无关

D与有关，与无关

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

线面角和二面角的求法

简答题（综合题）本大题共74分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 14分

20．函数在一个周期内的图像如图所示,为图像的最高点,、为图像与轴的交点，且为正三角形．

（1）求的值；

（2）若，且，求的值．

正确答案

（1）由已知可得:

又因正三角形ABC的高为2,则BC=4

所以,函数

（2）因为(1)有

由x0

所以,

故

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：简答题

分值: 16分

22．已知数列的前项和（）．

（1）求数列的通项公式；

（2）试构造一个数列（写出的一个通项公式）满足：对任意的正整数都有，且，并说明理由；

（3）设各项均不为零的数列中，所有满足的正整数的个数称为这个数列的变号数．令（），求数列的变号数．

正确答案

（1），

（2）要使，可构造数列，∵对任意的正整数都有，

∴当时，恒成立，即恒成立，即，

又，∴，∴，等等。

（3）解法一：由题设，

∵时，，

∴时，数列递增，

∵，由，

可知，即时，有且只有个变号数；

又∵，即，∴此处变号数有个。

综上得数列共有个变号数，即变号数为。

解法二：由题设，

当时，

；

又∵，∴时也有。

综上得数列共有个变号数，即变号数为。

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的判断与证明

题型：简答题

分值: 14分

21．在平面直角坐标系中，已知点、，是动点，且直线与的斜率之积等于．

（1）求动点的轨迹方程；

（2）设直线与分别与直线相交于点、，试问：是否存在点使得与的面积相等？若存在，求出点的坐标；若不存在，说明理由．

正确答案

（1）设点的坐标为，由题意得

化简得．

故动点的轨迹方程为

（2）解法一：设点的坐标为，点，得坐标分别为,．

则直线的方程为，直线的方程为

令得，．

于是的面积

又直线的方程为，，

点到直线的距离．

于是的面积

当时，得

又，所以=，

解得，因为，所以

故存在点使得与的面积相等，此时点的坐标为．

解法二：若存在点使得与的面积相等，设点的坐标为

则．

因为,

所以

即，

解得，因为，所以

故存在点使得与的面积相等，此时点的坐标为

解析

解析已在路上飞奔，马上就到！

知识点

两圆的公切线条数及方程的确定

题型：简答题

分值: 18分

23．若函数对任意的实数，均有，则称函数具有性质．

（1）判断函数是否具有性质，并说明理由；

（2）若函数具有性质,且．

①求证：对任意，都有；

②是否对任意，均有？若成立，请加以证明；若不成立，请给出反例并加以说明．

正确答案

（1）函数不具有性质．

例如，当时，，

又，

所以，，此函数不具有性质．

（2）①假设为中第一个大于的值

则，

因为函数具有性质，

所以，对于任意，均有

即，

则，

与矛盾

所以，对任意的有．

②不成立．

例如

证明：当为有理数时，均为有理数，

，

当为无理数时，均为无理数，

所以，函数对任意的，均有，

即函数具有性质．

当且为无理数时，．

所以“对任意均有”不成立．

如，，等

解析

解析已在路上飞奔，马上就到！

知识点

轨迹方程

题型：简答题

分值: 12分

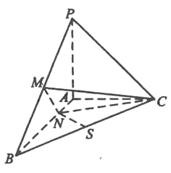
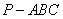
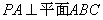
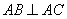
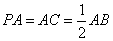
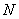
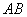
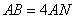
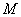
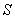
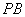
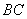
19．已知三棱锥中，，，，为上一点，，、分别为、的中点．

（1）求证：；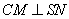

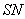
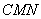
（2）求与平面所成角的大小．

正确答案

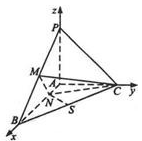
设PA=1，以A为原点，射线AB，AC，AP分别为x，y，z轴正向建立空间直角坐标系如图所示：

则P（0,0,1），C（0,1,0），B（2,0,0），M（1,0, ），N（ ,0,0），S（1, ,0）

（1），

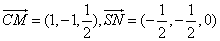
因为，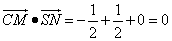

所以CM⊥SN

（2）, 设为平面CMN的一个法向量，

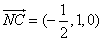
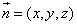
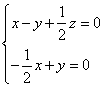
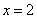
则，令，得

因为

所以SN与片面CMN所成角为45°。

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面垂直的判定与性质线面角和二面角的求法

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷