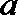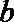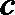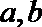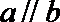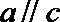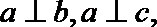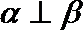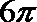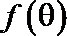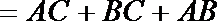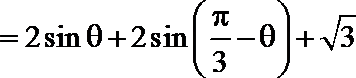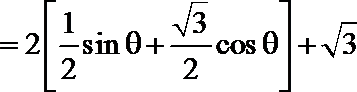- 真题试卷
- 模拟试卷
- 预测试卷
1.全集



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.用数学归纳法证明:“
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设等差数列







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知实数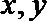
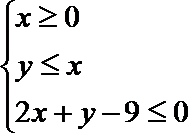
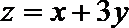
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.非零向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知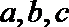
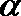
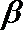
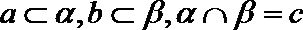
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.若存在实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.函数






①函数
②指数函数
③若



④在定义域上具有单调性的函数一定是单函数;
⑤若

其中的真命题是___________。(写出所有真命题的编号)
正确答案
②③④
解析
解析已在路上飞奔,马上就到!
知识点
11.已知下图是一个空间几何体的三视图,则该几何体的外接球的表面积为___________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知首项为正数的等差数列




正确答案
-3
解析
解析已在路上飞奔,马上就到!
知识点
19.已知等差数列




(1)求数列



(2)是否存在三个不等正整数


正确答案
解:(1)设前4项为
则
或
(2)
但

故不存在三个不等正整数
使

解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)求
(2)已知数列



(3)若



正确答案
解:(1)因

当



所以


(2)由(1)知,当


因为

令


即

(3)令

令



而

所以


当


当


所以


故
由题意有



解析
解析已在路上飞奔,马上就到!
知识点
20.如图,某工厂生产的一种无盖纸筒为圆锥形,现一客户订制该圆锥纸筒,并要求该圆锥纸筒的容积为π立方分米.设圆锥纸筒底面半径为r分米,高为h分米.
(1)求出r与h满足的关系式;
(2)工厂要求制作该纸筒的材料最省,求最省时
正确答案
解:(1)设圆锥纸筒的容积为

由该圆锥纸筒的容积为π,则

故r与h满足的关系式为
(2)工厂要求制作该纸筒的材料最省,即所用材料的面积最小,即要该圆锥的侧面积最小
设该纸筒的侧面积为



所以

设

由

当



因此,


由


解析
解析已在路上飞奔,马上就到!
知识点
16.已知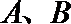
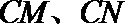
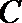
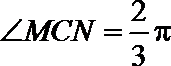
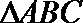
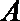
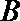
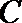
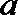
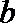
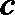
(1)若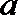
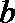
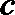
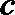
(2)若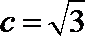
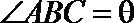

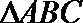
正确答案
解:(1)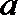
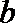
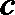
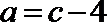
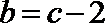
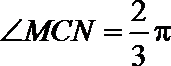
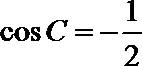
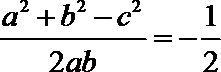
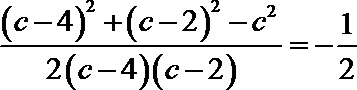
恒等变形得 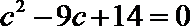
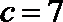
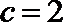
又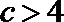
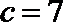
(2)在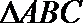
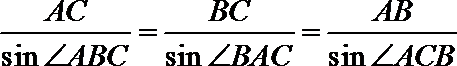
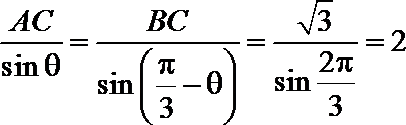
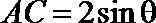
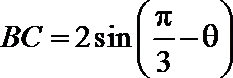
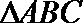
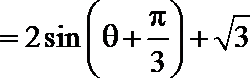
又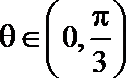
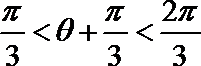

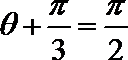
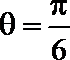
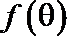
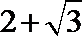
解析
解析已在路上飞奔,马上就到!
知识点
17.已知数列




正确答案
解:由

得


由

下面用数学归纳法证明:
(1)当
(2)假设当


那么
=
=
=
即
也就是说,当
结合(1)和(2)知命题成立.
解析
解析已在路上飞奔,马上就到!
知识点
18.在多面体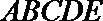
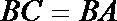
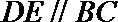
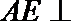
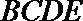
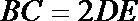
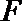
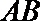
(I)求证: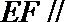
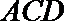
(II)若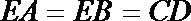
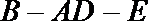
正确答案
证明:(Ⅰ)取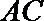
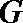
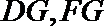
因为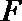
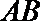
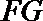
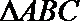
则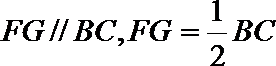
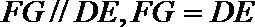
则四边形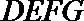
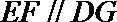
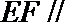
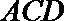
(Ⅱ)过点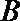
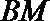
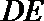
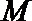
因为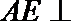
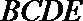
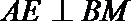
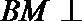
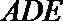
过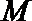
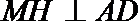

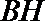
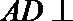
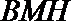
所以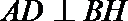
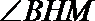
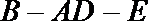
设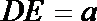
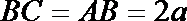
在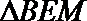
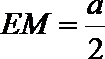
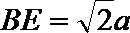
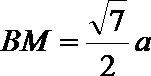
又因为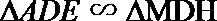
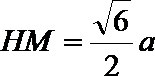
解析
解析已在路上飞奔,马上就到!