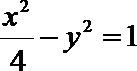- 真题试卷
- 模拟试卷
- 预测试卷
1. 抛物线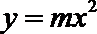
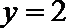
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若函数

正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
6.设函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 从长度分别为2、3、4、5的四条线段中任意取出三条,则以这三条线段为边可以构成三角形的概率是( )
正确答案
0.75
解析
解析已在路上飞奔,马上就到!
知识点
7.已知直线x=a(0<a<

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设x∈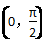
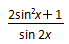
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知双曲线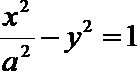
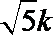
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. △ABC中,


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.在平面直角坐标系xOy中,点P是第一象限内曲线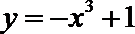
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.给出如下四个命题:
①

②

③函数




④ 若函数



其中正确的命题是( )(写出所有正确命题的题号)。
正确答案
③④
解析
解析已在路上飞奔,马上就到!
知识点
14.若关于


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知

(Ⅰ)求
(Ⅱ)求函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2。
(Ⅰ)求四棱锥P-ABCD的体积V;
(Ⅱ)若F为PC的中点,求证PC⊥平面AEF;
(Ⅲ)求证CE∥平面PAB。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点















(1)写出


(2)问食堂


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.幂函数y =
(1)求 a1的值;
(2)求数列 {an} 的通项公式 an;
(3)设 Sn为数列 {an} 的前 n 项和,若对于任意的实数 

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知点P(4,4),圆C:

A(3,1),


(Ⅰ)求m的值与椭圆E的方程;
(Ⅱ)设Q为椭圆E上的一个动点,求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知

(1)讨论

(2)求证:在(1)的条件下,
(3)是否存在实数


正确答案
解析
解析已在路上飞奔,马上就到!