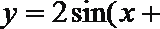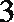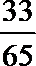- 真题试卷
- 模拟试卷
- 预测试卷
3. 设α、β、γ为不同的平面,m、n、l为不同的直线,则m⊥β的一个充分条件为( )
正确答案
解析
D . α⊥β,α∩β=l,m⊥l,根据面面垂直的判定定理可知,缺少条件m⊂α,故不正确;α∩γ=m,α⊥γ,β⊥γ,而α与β可能平行,也可能相交,则m与β不一定垂直,故不正确;α⊥γ,β⊥γ,m⊥α,而α与β可能平行,也可能相交,则m与β不一定垂直,故不正确;n⊥α,n⊥β,⇒α∥β,而m⊥α,则m⊥β,故正确,故选D.
知识点
4. 设等差数列





正确答案
解析
B 由等差数列性质知3、6-3、9-6成等差数列,即9,27,9-6成等差,∴9-6=45∴7+8+9=45,故选B.
知识点
6. 设



正确答案
解析
A ∵



知识点
2 .已知几何体的三视图如图,则该几何体的体积为( )
正确答案
解析
C.由已知可得该几何体是一个底面棱长为2侧面高为





知识点
1. 若复数




正确答案
解析
由(z-3)(2-i)=5,得z-3=


知识点
5.设
正确答案
解析
A 由0<




知识点
7.如图,一直线








正确答案
解析
A ∵












知识点
8.对于下列命题:
①命题“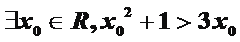
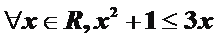
②在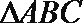
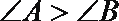

③设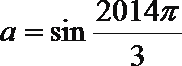


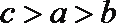
④将函数

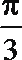
其中真命题的个数是( )
正确答案
解析
D
由全称量词存在量词得①正确,
在三角形内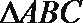
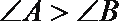
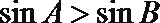
根据函数的周期性得到c>b>a, ③错误,
④三角函数图像的周期变换得到
知识点
9.已知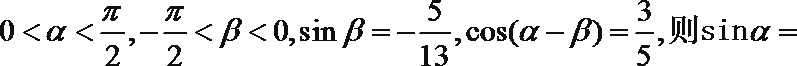
正确答案
解析
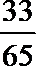
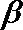
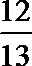
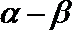

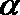
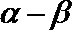
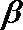
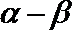
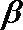
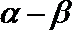
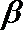
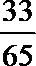
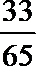
知识点
10. 已知函数

正确答案
0
解析
0 ∵由图形可知A=2,






知识点
12.已知
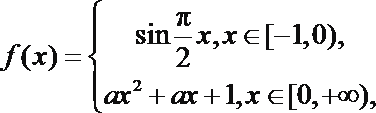
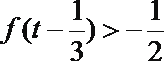
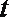
正确答案
(0,+∞)
解析
(0,+∞) 当x∈[-1,0)时,函数f(x)=sin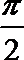




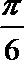







知识点
13.如图,多面体ABOARD,AB=CD=2,AD=BC=

①三棱锥O—ABC的体积是定值;
②球面经过点A、B、C、D四点的球的直径是
③直线OB//平面AC;
④直线AD与OB所成角是600;
⑤二面角A—AC—D等于300.
其中正确的结论是____________________。
正确答案
①②④
解析
①②④ 构造长方体,如右图,设A=x,OB=y,AC=z,则2+2=4,2+2=10,2+2=12,解得,x=1,y=








知识点
选做题(14 ~ 15题,只能从中选做一题)
14.(坐标系与参数方程选做题)
在极坐标系中,圆

15.(几何证明选讲选做题)
如图所示,过⊙O外一点A作一条直线与⊙O交于C,D两点,AB切⊙O于B,弦MN过CD的中点P.已知AC=4,AB=6,则MP·NP= ___________.
正确答案
14. 1
15.
解析
14. 1
圆ρ=2 即2+2=4,圆心为(0,0),半径等于2. 直线 


15. 
∵AB为⊙O的切线,AC为⊙O的割线由切割线定理可得:AB=AC•AD由AC=4,AB=6,故AD=9故CD=5 又∵N是弦CD的中点故PC=PD=

知识点
11.过点




正确答案
解析









知识点
18.如图,在三棱锥





(Ⅰ)求证:DE⊥平面
(Ⅱ)当二面角
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知
(1)求f(x)的周期及其图象的对称中心;
(2)△ABC中,角A、B、C所对的边分别是


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
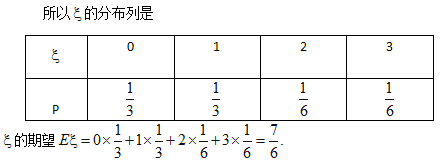
17.甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲、乙、丙面试合格的概率分别是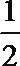
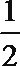
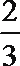
(Ⅰ)至少有1人面试合格的概率;
(Ⅱ)签约人数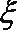
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 如图,四棱柱








(Ⅰ)证明:平面

(Ⅱ)若


(Ⅲ)在(Ⅱ)的条件下,试求二面角
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.等比数列{





(1)求r的值;
(2)当b=2时,记 


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)当


(2)当


(3)求证:

正确答案
解析
解析已在路上飞奔,马上就到!