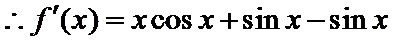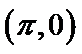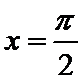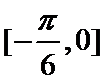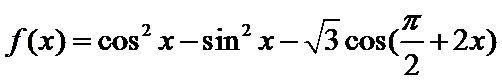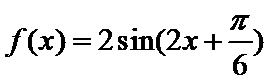- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合


正确答案
解析
集合M中的代表元素为y,y的取值范围为


考查方向
解题思路
理解集合M和集合N中元素的特点
易错点
集合中元素的特征,集合N中代表元素理解错误
知识点
3.中、美、俄等21国领导人合影留念,他们站成两排,前排11人,后排10人,中国领导人站在第一排正中间位置,美俄两国领导人站在与中国领导人相邻的两侧,如果对其他领导人所站的位置不做要求,那么不同的站法共有( )
正确答案
解析
先排中国领导人,只有一种选择;再排美俄领导人,有


考查方向
解题思路
先排中国领导人,只有一种选择;再排美俄领导人
知识点
4.执行如图所示的程序框图,若输入n的值为8,则输出S的值为( )
正确答案
解析
当i=2,k=1时,s=2;
当i=4,k=2时,s=4
当i=6,k=3时,s=8
当i=8,k=4时,不满足条件i<8,退出循环,则输出的s=8,故选择B
考查方向
解题思路
顺序结构 循环结构 判断结构
易错点
循环语句理解错误,判断条件看错
知识点
5.等比数列


正确答案
解析
等比数列中,
所以

考查方向
解题思路
利用等比数列项和项数的关系,进而求解
易错点
利用等比数列前N项和公式求解,找a1和公比q,使试题复杂。
知识点
9.不等式组

正确答案
解析
如图所示,作出不等组的可行域,根据几何概型的定义,可知红色区域面积与四边形ABCD的面积的比就是所求概率。红色区域面积不好求,由于是选择题,可以根据选项求得,容易得到,红色区域的面积比四边形面积的一半少,比四分之一多,所以结合选项,选择D
考查方向
解题思路
分别求出两个不等式组所表示的区域的面积,然后利用集合概型相关性质计算求得
易错点
区域求面积,不等式取值区间
知识点
10.已知一个几何体的三视图如右图所示,则该几何体的体积为( )
正确答案
解析
根据几何体的三视图,可知,立体图形是以高为2,底面积为2的两个集合组合体,根据几何体的体积公式利用底面积乘以高求得,所以选D
考查方向
解题思路
本题考查由三视图还原几何体并且看出几何体各个部分的长度,本题解题的关键是要求体积需要求出几何体的底面面积和高,三棱锥的高是由垂直与底面的侧面的高得到,本题是一个基础题.
知识点
11. 已知双曲线




正确答案
解析
利用交点这一突破口,建立方程关系,进而求出a和c的关系,所以得到离心率为
考查方向
解题思路
先设交点坐标,与渐近线联立方程组,最后用余弦定理求得
易错点
计算错误、离心率、渐近线方程错误
知识点
2.复数

正确答案
解析


考查方向
解题思路
将复数z转换成a+bi的形式,然后求出
易错点
混淆

知识点
6.若非零向量




正确答案
解析

又因为

考查方向
解题思路
根据垂直关系得到向量
易错点
向量垂直与向量积的关系
知识点
8. 设函数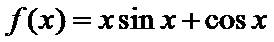
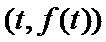
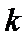
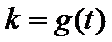
正确答案
解析
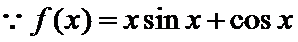
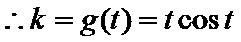
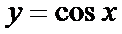
考查方向
解题思路
先求导数,然后利用导函数求k的解析式,进而判断函数图象
易错点
求导错误,函数单调性不会判断
知识点
12.已知函数


正确答案
解析
由题意得,函数在f(x)在x=1处取到最小值。










令








即
考查方向
解题思路
先判断函数的单调性,然后求导求最值。
易错点
函数单调性判断错误、求导错误
知识点
7.定义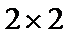
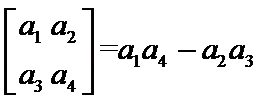
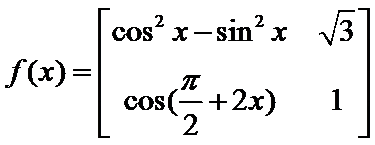
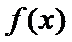
正确答案
解析
根据矩阵的定义,可以得到
所以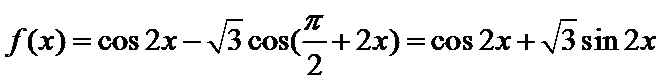
根据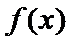
考查方向
三角函数
解题思路
先根据矩阵的定义,得到f(x)的解析式,然后根据函数的解析式判断函数的相关性质.
易错点
三角函数公式记忆混淆
知识点
13.已知随机变量X服从正态分布X~N(2,σ2), P(X<4)=0.84, 则P(X≤0)的值为 .
正确答案
0.16
解析
因为随机变量X服从正态分布

考查方向
解题思路
根据正态分布的概率性质求解
易错点
对正态分布的相关性质的理解
知识点
14.若


正确答案
2
解析
因为

所以






考查方向
解题思路
根据展开式 求a和b的关系
易错点
展开式公式记错、基本不等式“一正”“二定”“三相等”
知识点
15. 已知在



正确答案
解析
因为



考查方向
解题思路
由正弦定理整理,二倍角正弦公式
易错点
正弦定理的转化
知识点
16.一个空心球玩具里面设计一个棱长为4的内接正四面体,过正四面体上某一个顶点所在的三条棱的中点作球的截面,则该截面圆的面积是 .
正确答案
解析
易求截面圆的半径为
考查方向
解题思路
先根据正四面体的棱长求出其外接球的半径,根据相似比等性质,求出截面圆的半径。
易错点
误以为正四面体三条棱的中点做截面就是所求截面,其实不然
知识点
20. 已知F(







(Ⅰ)求抛物线方程和N点坐标;
(Ⅱ)判断直线




正确答案
见解析
解析
(Ⅰ)由题意

故抛物线方程为
由|NF|=

∵
∴
所以N(2,2)。
(Ⅱ)由题意知直线的斜率不为0,则可设直线

联立方程组

设两个交点A(





由

此时,
故直线


因为M(2,-2),
所以M,E所在直线平行x轴,
所以△MAB的面积



考查方向
解题思路
建立适当的坐标系,利用直线斜率之间的关系建立方程,进而求解,与抛物线联立成方程组,整理可得。
易错点
计算能力弱,找不到面积最小时候的情况
知识点
21. 已知函数
(Ⅰ)设函数

(Ⅱ)若不等式


正确答案
见解析
解析
(Ⅱ)
①当


令




②当



综上,当



当

(Ⅱ)由题意可知,不等式

即在[1,e]存在

由(Ⅰ)中

即函数
由(Ⅰ)知,当

当
①当


②当



③当






综上可得,实数

考查方向
解题思路
确定函数的定义域,利用导数求函数的单调区间,根据题意构造出恰当的不等式,进而求出参数的取值范围。
易错点
求导错误,构造函数不成功。
知识点
17. 在等差数列



(Ⅰ)求数列

(Ⅱ)求数列

正确答案
见解析
解析
(Ⅰ)设等差数列




当n=1时,
当n


所以,数列
(Ⅱ)n=1时,
n

所以

综上,
考查方向
解题思路
利用构造的等比数列求前n项和公式的求解
易错点
构造等比数列
知识点
18. 现有甲、乙两个靶,某射手向甲靶射击一次,命中的概率为

(Ⅰ)求该射手恰好命中一次的概率;
(Ⅱ)求该射手的总得分

正确答案
见解析
解析
(Ⅰ)记“该射手恰好命中一次”为事件



由题意知,

由于
(Ⅱ)根据题意,

根据事件的独立性和互斥性得



故
所以
考查方向
解题思路
第一问将所有可能的情况列举出求解,第二问根据随机变量分布列的概念及特征,一次写出当随机变量取不同值得情况
易错点
列举情况不全面
知识点
19. 如图,三棱柱ABC-A1B1C1所有的棱长均为2,B1在底面上的射影D在棱长BC上,且A1B∥平面ADC1。
(Ⅰ)求证:平面ADC1⊥平面BCC1B1;
(Ⅱ)求平面ADC1与平面A1AB所成角的正弦值.
正确答案
见解析
解析
(Ⅰ)连接A1C交AC1于点O,连接OD,则平面A1BC∩平面ADC1=OD。∵A1B∥平面ADC1,∴A1B∥OD,又为O为A1C的中点。
∴D为BC的中点,则AD⊥BC。
又B1D⊥平面ABC,∴AD⊥B1D,BC∩B1D=D。
∴AD⊥平面BCC1B1。
又AD
(Ⅱ)以D为坐标原点,DC,DA,DB1所在的直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则D(0,0,0),B(-1,0,0),A(0,


易知




则




易知





∴cos<




那么平面ADC1与平面A1AB所成角的正弦值为
考查方向
解题思路
通过线面垂直证明面面垂直,找到二面角的平面角构造三角形,进而计算出二面角的平面角的余弦值
易错点
找不到垂直关系,找不到二面角
知识点
22.如图,AB为圆O的直径,BE为圆O的切线,点C为圆O上不同于A、B的一点,AD为∠BAC的平分线,且分别与BC交于H,与圆O交于D,与BE交于E,连结BD、CD.
(Ⅰ)求证:BD平分∠CBE;
(Ⅱ)求证:
正确答案
见解析
解析
证明:
(I)由弦切角定理得到∠DBE=∠DAB,又∠DBC=∠DAC,∠DAB=∠DAC,所以∠DBE=∠DBC,即BD平分∠CBE.
(Ⅱ)由(I)可知BE=BH,所以
所以


考查方向
解题思路
利用弦切角定理找出与其相等的角,并进行相等角间转化;利用相似三角形的判定定理判定△AHC∽△AEB;利用相似三角形对应边成比例,证明有关问题.
易错点
辅助线的作法,相似条件找不准