- 真题试卷
- 模拟试卷
- 预测试卷
4.已知二次函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.六张卡片上分别写有数字1,1,2,3,4,5,从中取四张排成一排,可以组成不同的四位奇数的个数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.将三颗骰子各掷一次,设事件A=“三个点数都不同“,B=“至少出现一个6点”,则条件概率P(A|B),P(B|A)分别是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若i为虚数单位,下图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,则复数的共轭复数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知三个不等式:
①x2-4x+3<0;
②x2-6x+8>0;
③2x2-8x+m≤0。
要使同时满足①式和②式的所有x的值都满足③式,则实数m的取值范围是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.执行如图所示的程序框图,如果输出S=3,那么判断内应填入的条件是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在区间[1,5]和[2,6]内分别取一个数,记为a和b,则方程

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知P(x,y)是直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知椭圆


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.点P是双曲线






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为ξ,求ξ的分布列与期望。
下面的临界值表供参考:
(参考公式:K2=
正确答案
(1)列联表补充如下:
(2)∵K2=
∴在犯错误的概率不超过0.005的前提下,认为喜爱打篮球与性别有关.
(3)喜爱打篮球的女生人数ξ的可能取值为0,1,2.
其概率分别为
P(ξ=0)=
P(ξ=1)=
P(ξ=2)=
故ξ的分布列为:
ξ的期望值为:Eξ=0×


解析
解析已在路上飞奔,马上就到!
知识点
20.从装有大小相同的2个红球和6个白球的袋子中,每摸出2个球为一次试验,直到摸出的球中有红球(不放回),则试验结束。
(1)求第一次试验恰摸到一个红球和一个白球概率;
(2)记试验次数为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆



(1)求椭圆
(2)设O为坐标原点,点A,B分别在椭圆



正确答案
(1)由已知可设椭圆
其离心率为
故
则
故椭圆的方程为
(2)解法一 
由




因此可以设直线
将

得
所以
将

则
所以
由
得
即
解得
故直线

解法二 
由




因此可以设直线
将

得
所以
由
得
将

得
即
解得
故直线


解析
解析已在路上飞奔,马上就到!
知识点
17.已知全集U=R,非空集合


(1)当

(2)命题

正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
18.设
(1)当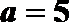
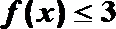
(2)当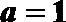
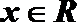
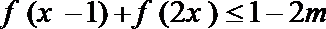

正确答案
(1)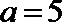
即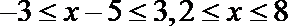
所以解集为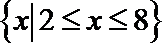
(2)当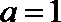
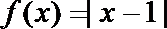
令
由图像知:
当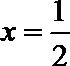
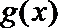

由题意知: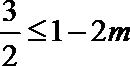
所以实数

解析
解析已在路上飞奔,马上就到!
知识点
22.如图,已知抛物线










(1)求抛物线
(2)当


(3)若直线



正确答案
(1)∵点

∴

(2)法一:∵当


∴
设

∴
∴ 
∴

法二:∵当


∴


∴直线

联立方程组
得
∵
∴

同理可得

∴
(3)法一:设
∵
∴
可得,直线

同理,直线

∴

∴直线

令
可得
∵


∴
法二:设点


以


⊙

①-②得:
直线

当
直线


∵


∴
解析
解析已在路上飞奔,马上就到!
知识点
13.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若不等式组

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.对大于或等于2的自然数 m的n 次方幂有如下分解方式:
22=1+3,
32=1+3+5,
42=1+3+5+7;
23=3+5,
33=7+9+11,
43=13+15+17+19.
根据上述分解规律,若n2=1+3+5+…+19, m3(m∈N*)的分解中最小的数是21,则m+n的值为_______。
正确答案
15
解析
解析已在路上飞奔,马上就到!
知识点
16.已知


正确答案
解析
解析已在路上飞奔,马上就到!