- 真题试卷
- 模拟试卷
- 预测试卷
1.集合P={3,4,5},Q={6,7},定义

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.在第29届北京奥运会上,中国健儿取得了51金、21银、28铜的好成绩,稳居金牌榜榜首,由此许多人认为中国进入了世界体育强国之列,也有许多人持反对意见,有网友为此进行了调查,在参加调查的2548名男性中有1560名持反对意见,2452名女性中有1200名持反对意见,在运用这些数据说明性别对判断“中国进入了世界体育强国之列”是否有关系时,用什么方法最有说服力( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.定义在R上的连续函数f(x)满足f(-x)=-f(x+4),当x>2时,f(x)单调递增,如果x1+x2<4,且(x1-2)(x2-2)<0,则f(x1)+f(x2)的值 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 设向量a,b,c满足

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.如图给出的是计算
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.一个几何体的三视图如右图所示,则该几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.过





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.过双曲线
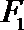
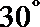
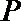
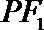
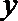
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.点







①
②

③曲线


其中真命题的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.如果把四个面都是直角三角形的四面体称为“三节棍体”,那么从长方体八个顶点中任取四个顶点,则这四个顶点是“三节棍体”的四个顶点的概率为___________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.在△ABC中,a、b、c分别为∠A、∠B、∠C的对边,三边a、b、c成等差数列,且B=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为___________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.对于实数a和b,定义运算“﹡”:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.设数列



(1)若

(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数f(x)=
(I)设函数F(x)=f(x)-g(x),求F(x)的单调区间;
(II)若存在常数k,m,使得f(x)≥kx+m,对x∈R恒成立,且g(x)≤kx+m,
对x∈(0,+∞)恒成立,则称直线y=kx+m为函数f(x)与g(x)的“分界线”,
试问:f(x)与g(x)是否存在“分界线”?若存在,求出“分界线”的方程,若不存在,请说明理由。
正确答案
(I)由于函数f(x)=
因此,F(x)=f(x)-g(x)=
则


当0<x<


当x>



因此,函数F(x)的单调减区间是(0,


(II)由(I)可知,当x=

则f(x)与g(x)的图象在x=


假设f(x)与g(x)存在“分界线”,则其必过点(

故设其方程为:

由f(x)≥

所以,
因此k=
下面证明g(x)≤
设G(x)=

所以当0<x<



当x=

故所求“分界线“的方程为:
解析
解析已在路上飞奔,马上就到!
知识点
18.在如图所示的几何体中,四边形ABDE为梯形,AE//BD,AE

(I)求证:CM
(II)求锐二面角
正确答案

解析
解析已在路上飞奔,马上就到!
知识点
19.衡水市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰。若现有500人参加测试,学生成绩的频率分布直方图如下:
(I)求获得参赛资格的人数;
(II)根据频率直方图,估算这500名学生测试的平均成绩;
(III)若知识竞赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛,已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为
求甲在初赛中答题个数的分布列及数学期望.
正确答案
(I)获得参赛资格的人数
(II)平均成绩:
(III)设甲答对每一道题的概率为.P
则

解析
解析已在路上飞奔,马上就到!
知识点
20.已知抛物线














(1)求证:

(2)若











正确答案
(1)设


所以



所以






(2)设

由
同理
所以面积
设

由


得到

②得

所以当


所以当




所以

解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24三题中任选一题做答。如果多做,则按所做的第一题记分.
22.选修4-1:几何证明选讲
如图,AB为圆




(I)求证:

(Ⅱ)求证:CD2=CF·CP.
23.选修4—4:坐标系与参数方程
在平面直角坐标系





(I)求|AB|的值;
(Ⅱ)求点M(-1,2)到A、B两点的距离之积.
24.选修4—5:不等式选讲
已知函数
(I)求不等式
(Ⅱ)若关于



正确答案
22.(Ⅰ) 
所以在 

在 
所以
(Ⅱ)在

由①得


∴
所以CD2=CF·CP
23. (Ⅰ)
则




(Ⅱ)
24.不等式的解集为
(II)
解析
解析已在路上飞奔,马上就到!