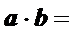- 真题试卷
- 模拟试卷
- 预测试卷
已知数列



17.求证:数列
18.若不等式

正确答案
(1)∵



解析
证明:∵


所以数列
考查方向
解题思路
通过“构造法”来证明
易错点
通过“构造法”来证明
正确答案

解析
解:由(1)知,







考查方向
解题思路
涉及恒成立问题,转化成求函数的最值.
易错点
转化成求函数的最值.
如图,菱形ABCD中,∠ABC = 60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB = AE = 2。
21.求证:BD⊥平面ACFE;
22.当直线FO与平面BED所成角的大小为45°时,求CF
正确答案
略;
解析
证明:









考查方向
解题思路
根据线面垂直的判定定理,在平面ACFE中寻找两条与BD垂直的直线;
易错点
本题容易因对频率分布直方图的认识不到位而导致计算出错;
正确答案
a=3;
解析
解:如图以






设平面

则有
即


由题意


由
考查方向
解题思路
可以通过建立空间直角坐标系,用向量的方法来解决;
易错点
本题容易因对频率分布直方图的认识不到位而导致计算出错;
已知椭圆C:


23.求椭圆C的方程;
24.直线l经过点

正确答案

解析
由题意得
解得
所以

考查方向
解题思路
根据椭圆的标准方程以及几何性质,建立方程组,通过待定系数的方法即可求解;
正确答案
存在

解析
存在

当直线

设直线




所以



所以
不妨设
因为

从而


综上,
考查方向
解题思路
可以通过直线与椭圆的位置关系建立方程组,利用韦达定理、解方程求解;
已知函数


25.求a,b的值;
26.求函数

27.证明:当x > 0时,
正确答案

解析

由题设得,

得,
考查方向
解题思路
根据导数的几何意义,建立方程组,通过“待定系数法”即可求解;
易错点
通过“待定系数法”求解
正确答案

解析
由(Ⅰ)知,

故


考查方向
解题思路
可以通过函数的单调性与导数的关系,利用导数判断函数的单调性,再结合函数的单调性确定函数的最大值;
正确答案
略。
解析
因为








下证:当

设

由(Ⅱ)知,


又
所以,存在

所以,当



故



又

故
由(Ⅱ)知,


所以,
即

即

考查方向
解题思路
可以通过转化化归的方法,将问题转化为函数的最大、最小值问题进行求解。
在直角坐标系xOy中,直线l的方程是y = 8,圆C的参数方程是
30.求直线l和圆C的极坐标方程;
31.射线OM:θ = α(其中


正确答案
直线



解析
直线

圆

所以圆

考查方向
解题思路
根据三种方程之间的相互关系进行转化。
易错点
根据三种方程之间的相互关系进行转化。
正确答案

解析
依题意得,点


所以

从而

所以
故当


考查方向
解题思路
根据相关知识求出|OP|、|OQ|、|OM|、|ON|的值,然后利用三角函数的知识求最值。
易错点
利用三角函数的知识求最值。
在某批次的某种日光灯管中,随机地抽取500个样品,并对其寿命进行追踪调查,将结果列成频率分布直方图如下。根据寿命将灯
19.根据这500个数据的频率分布直方图,求出这批日光灯管的平均寿命;
20.某人从这个批次的灯管中随机地购买了4个进行使用,若以上
正确答案
370;
解析
平均数为
考查方向
解题思路
根据频率分布直方图的相关知识求出平均值;解:平均数为
易错点
本题容易因对频率分布直方图的认识不到位而导致计算出错;
正确答案
随机变量
数学期望
解析





所以




所以随机变量
所以

考查方向
解题思路
求出随机变量X取不同值时的概率,列出随机变量的分布列;根据数学期望的计算公式求出相应的数学期望.
易错点
本题容易因对频率分布直方图的认识不到位而导致计算出错;
如图,EF是⊙O的直径,AB∥EF,点M在EF上,AM、BM分别交⊙O于点C、D。设⊙O的半径是r,OM = m。
28.证明:
29.若r = 3m,求
正确答案
(1)略;
解析
作





因为

所以
从而
故
考查方向
解题思路
本题考查几何证明选讲的相关知识,解题步骤如下:根据图形做辅助线,利用线段之间的关系进行转化。
正确答案
解析
因为

所以
因为
所以
又因为

考查方向
解题思路
利用相交弦定理解决长度的问题。
易错点
利用相交弦定理解决长度的问题。
3.若m = 6,n = 4,按照如图所示的程序框图运行后,输出的结果是
正确答案
解析
将m = 6,n = 4,代入流程图中,由于6>4,因此走左边的一支,此时
考查方向
解题思路
根据流程顺序,将m,n的值代入验证即可。
易错点
本题会由于没有记清楚
知识点
1.若集合

正确答案
解析


考查方向
本题主要考查了集合的运算、一元二次方程的解法以及区间的认识,集合的基本运算在近几年的各省高考题出现的频率较高,常与一元二次不等的解法交汇命题。
解题思路
先求出集合B,然后根据交集的定义求出相应的结果。
易错点
集合的运算、一元二次方程的解法
知识点
2.若复数z满足zi = 1 + i,则z的共轭复数是
正确答案
解析
在zi = 1 + i两边同时乘以i,得到 -z=i-1,从而z=1-i,于是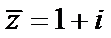
考查方向
解题思路
先求出复数z,然后根据共轭复数的概念写出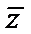
易错点
复数的运算题目一般比较容易,往往会在计算时因失误而失分。
知识点
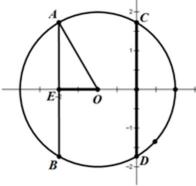
4.已知向量a,b满足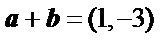
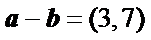
正确答案
解析
由于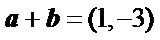

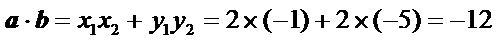
考查方向
解题思路
1、根据向量的加、减运算计算出向量a,b的坐标;
2、由向量数量积的坐标运算公式
易错点
1、本题往往会因为没有记清楚向量数量积的坐标运算公式而出错;
2、本题会在计算时出现失误而导致计算出错。
知识点
5.若函数

正确答案
解析
因为1>0,所以


考查方向
解题思路
根据复合函数的运算规则,从内层函数出发,逐层往外计算,因此先算

易错点
本题易在不理解
知识点
6.设


正确答案
解析
因为





考查方向
解题思路
1、充分条件的判断可以通过取特殊值进行验证;
2、必要条件的判断可以通过不等式的基本性质进行判断。
易错点
1、本题易在不理解充分条件与必要条件的含义而导致错误。
2、本题在应用不等式的性质时会因为疏忽符号而出现错误。
知识点
9.从某大学随机抽取的5名女大学生的身高x(厘米)和体重y(公斤)数据如下表 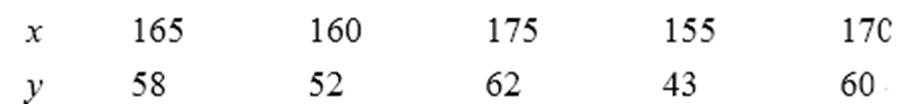
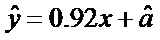
正确答案
解析
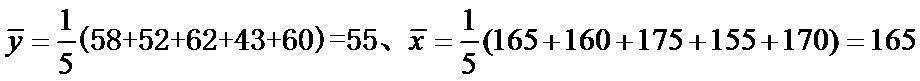
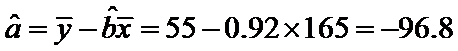
考查方向
解题思路
根据公式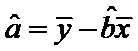

易错点
1、本题易在计算时出现失误而导致错误。2、本题不容易理解线性回归直线方程的含义而导致无法做答。
知识点
10.已知某几何体的三视图如图所示,则该几何体的表面积为
正确答案
解析
该三视图所对应得空间几何体如图所示:根据台体的体积计算公式
考查方向
解题思路
1、首先根据三视图还原出原来的几何体;
2、根据空间几何体的体积计算公式选择合适的公式计算。
易错点
不能根据三视图准确地还原出原来的空间几何体而导致本题不会做。
知识点
11.双曲线C:




正确答案
解析
由于MN∥F1F2,





考查方向
解题思路
确定N、Q的坐标,代入双曲线方程,即可求出双曲线的离心率。
易错点
本题容易因为对双曲线的性质记忆不清楚而导致题目无法进行。
知识点
12.已知定义在R上的奇函数







正确答案
解析
由












考查方向
解题思路
根据题目中的信息画出符合条件的函数的草图,结合草图利用函数的周期性予以解决。
易错点
本题容易因为不理解
知识点
7.若点


正确答案
解析
因为点




考查方向
解题思路
首先由点P在直线上,可以求得
易错点
1、本题易在使用诱导公式时判断错误符号而导致出错。
2、本题容易因为公式记忆不清楚而出现错误。
知识点
8.数学活动小组由12名同学组成,现将12名同学平均分成四组分别研究四个不同课题,且每组只研究一个课题,并要求每组选出一名组长,则不同的分配方案的种数为
正确答案
解析
第一步,先给每个课题选研究成员,共有


考查方向
解题思路
确定解决问题的步骤,根据步骤逐步完成任务即可。
易错点
本题易在左右平移时发生错误,易忽视x的系数2 。
知识点
13.若实数x,y满足

正确答案
2
解析
可行域如图所示,易知当直线

考查方向
解题思路
1、根据线性约束条件画出可行域。
2、画出直线
易错点
本题往往会因为不能准确地画出可行域而导致错误。
知识点
15.已知圆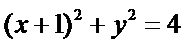

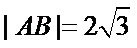
正确答案
8
解析
在平面直角坐标系中画出圆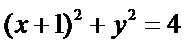
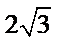
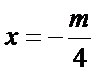
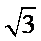
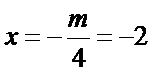
考查方向
解题思路
根据题意画出合适的图形,然后结合图形进行分析和计算.
易错点
本题必须要对抛物线的标准方程和几何性质有深刻的认识,否则容易因为误认为准线为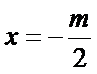
知识点
14.已知三棱锥P-ABC,若PA,PB,PC两两垂直,且PA = 2,PB = PC = 1,则三棱锥P-ABC的内切球半径为__________。
正确答案
解析
如图设O为内切球的球心,其半径为r,则由

考查方向
解题思路
以内切球的球心为顶点,把三棱锥转化成4个小三棱锥,然后体积加一起就是大三棱锥的体积。(本题也可以)
易错点
本题往往会因为不能准确地想象题目中所要求的空间几何体而无法求解。
知识点
16.已知ΔABC满足

正确答案
[1,3]
解析
由
整理得:
由
得
将(1)代入(2)得到
三角形BCM中余弦定理可得
(3)、(4)联立整理得
三角形ACM中余弦定理可得
将(1)、(3)、(5)代入(6)得
因此
考查方向
解题思路
1、根据
2、结合图形利用正余弦定理分析求解
易错点
结合图形利用正余弦定理分析求解