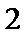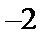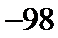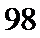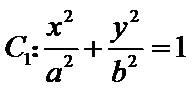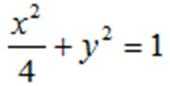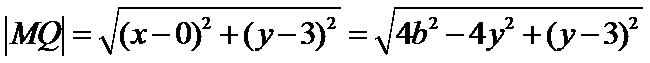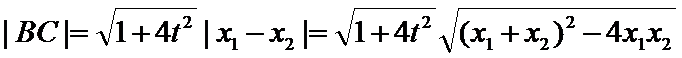理科数学广州市2016年高三期末试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

1．若全集U=R，集合，，则＝（）

正确答案

解析

=（0，2），=[1,+∞），C=(-∞,1），=(0,1)

考查方向

本题主要考查了指数不等式的解法，以及集合的交集补集的概念。

解题思路

分别将A B集合化简过后求解即可

易错点

本题易在化简A集合时出错。

知识点

交、并、补集的混合运算

题型：单选题

分值: 5分

2．已知，是虚数单位，若与互为共轭复数，则（）

正确答案

解析

∵与共轭 ∴a=2 b=1

考查方向

本题主要考查了共轭复数的概念：实部相等虚部互为相反数，及复数的基本运算。近几年复数再高考中常出现于选择题，属于容易题。

解题思路

由共轭复数的概念确定a b的值然后求解

易错点

本题需注意。

知识点

复数的基本概念复数代数形式的乘除运算

题型：单选题

分值: 5分

3．下列说法中正确的是（）

A“”是“函数是奇函数”的充要条件

B若，则

C若为假命题，则，均为假命题

D命题“若，则”的否命题是“若，则”

正确答案

解析

A 错误，既非充分也非必要。原概念：B 错误。C 错误。即p且q是假，只能说明p q中至少一个假，并不能说明都假，所以C错D 正确。注意否命题条件与结论都要否

考查方向

本题主要考查了简易逻辑部分的四个命题的关系，以及真假命题的判定。

解题思路

紧扣定义，逐个判定。

易错点

概念模糊造成失误。

知识点

命题的真假判断与应用

题型：单选题

分值: 5分

5．执行如图所示的程序框图，输出的结果为（）

正确答案

解析

初始值 x=1 y=1 k=0

第一次循环 s=x-y=0 t=x+y=2 x=s=0 y=t=2 k=k+1=1<3 继续循环

第二次循环 s=x-y=-2 t=x+y=2 x=s=-2 y=t=2 k=k+1=2<3继续循环

第三次循环 s=x-y=-4 t=x+y=0 x=s=-4 y=t=0 k=k+1=3终止循环

x= -4 y=0

输出

考查方向

本题主要考查算法部分流程图的解读，高考必考一道小题。

解题思路

按照流程图，一次一次循环输出结果。

易错点

由于变量较多，粗心失误。

知识点

程序框图

题型：单选题

分值: 5分

4．已知在上是奇函数,且满足,当时,，则（）

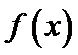
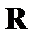
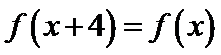
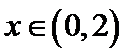
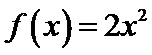
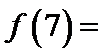
正确答案

解析

f(7)= f(4+3)=f(3)=- f(-3)=- f(4-3)=- f(1)

f(1)可代入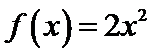中求解

考查方向

本题主要考查函数的周期性与奇偶性。

解题思路

利用周期性以及奇偶性将问题转化到（0，2）区间解决。

易错点

将f(7)转化到f(3)后无从下手

知识点

函数奇偶性的性质函数的周期性函数的值

题型：单选题

分值: 5分

6．各项均为正数的等差数列中，，则前12项和的最小值为（）

正确答案

解析

考查方向

本题主要考查等差数列的性质、求和公式，及均值不等式的应用。

解题思路

注意观察项数（下角标）的关系1+12=4+9。

易错点

无法充分利用条件，将条件引向结论。

知识点

等差数列的性质及应用利用基本不等式求最值

题型：单选题

分值: 5分

7．一个几何体的三视图如图所示，其中正视图与侧视图都是斜边长为2的直角三角形，俯视图是半径为1的四分之一圆周和两条半径，则这个几何体的体积为（）

正确答案

解析

通过观察判断该几何体是一个圆锥的四分之一高是

考查方向

本题主要考查三视图的观察能力。

解题思路

通过三视图的观察判断形状。

易错点

图形观察失误。

知识点

组合几何体的面积、体积问题简单空间图形的三视图

题型：单选题

分值: 5分

8．已知，且，函数的图像的相邻两条对称轴之间的距离等于，则的值为（）

正确答案

解析

三角函数相邻两对称轴正好跨度了半个周期所以

，， =

又，且，所以

考查方向

本题主要考查三角函数的周期性质、诱导公式、同角三角函数。

解题思路

利用堆成轴间距求出周期确定，然后利用诱导公式求解。

易错点

无法利用条件确定周期进而求解。

知识点

正弦函数的对称性由y=Asin（ωx+φ）的部分图象确定其解析式

题型：单选题

分值: 5分

9．若实数满足约束条件则的取值范围是（）

正确答案

解析

画图找到可行域，从图上可以观察出在C点最大，在A点最小。

求解坐标A（1，2） C（1．5，1）

考查方向

本题主要考查线性规划问题，以及目标函数的几何意义

解题思路

画图找出可行域，明确目标函数即过原点的直线斜率的倒数。

易错点

无法正确找出可行域以及明白目标函数的意义。

知识点

其它不等式的解法

题型：单选题

分值: 5分

10．过双曲线的一个焦点作一条渐近线的垂线，垂足为点，与另一条渐近线交于点，若，则此双曲线的离心率为（）

正确答案

解析

考查方向

本题主要考查双曲线的简单性质

解题思路

由得出A为线段FB的中点，再借助于图象分析出其中一条渐近线对应的倾斜角的度数，找到a，b之间的等量关系，进而求出双曲线的离心率．

易错点

无法找出角度关系，进而推导斜率问题。

知识点

双曲线的几何性质

题型：单选题

分值: 5分

12．已知的三个顶点，，的坐标分别为，O为坐标原点，动点满足，则的最小值是（）

正确答案

解析

考查方向

本题主要考察平面向量的坐标运算以及向量相关的几何意义。

解题思路

将向量问题转化为解析几何问题解题

易错点

无法正确计数。

知识点

平面向量数量积的运算向量在几何中的应用

题型：单选题

分值: 5分

11．将5位同学分别保送到北京大学，上海交通大学，中山大学这3所大学就读，每所大学至少保送1

人，则不同的保送方法共有（）

A150种

B180种

C240种

D540种

正确答案

解析

考查方向

本题主要考查计数原理的应用。

解题思路

注意分类讨论计算

易错点

无法正确计数，不清楚何时用组合数何时用排列数。

知识点

排列、组合及简单计数问题

填空题本大题共5小题，每小题5分，共25分。把答案填写在题中横线上。

题型：填空题

分值: 5分

13．已知向量，满足，在方向上的投影是，则．

正确答案

解析

考查方向

本题主要考察平面向量的投影的概念以及数量积。

解题思路

易错点

。

知识点

平面向量数量积的运算

题型：填空题

分值: 5分

14．已知，则．

正确答案

解析

考查方向

本题主要考察三角函数诱导公式及二倍角公式。

解题思路

首先利用诱导公式将条件及结论化简，观察条件与结论的关系，然后选取正确的公式计算。

易错点

诱导公式失误。

知识点

三角函数的化简求值诱导公式的作用二倍角的余弦

题型：填空题

分值: 5分

16．已知为R上的连续可导函数，且，则函数
的零点个数为___________．

正确答案

解析

考查方向

本题主要考察导数与函数单调性的关系以及零点的求法。

解题思路

易错点

无法从条件中捕捉到有效信息，向结论靠拢。

知识点

函数零点的判断和求解导数的运算

题型：填空题

分值: 12分

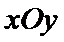
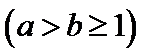
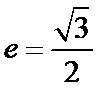
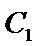
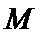
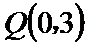
20．在平面直角坐标系中，已知椭圆的离心率，且椭圆上一点到点的距离的最大值为4．

（Ⅰ）求椭圆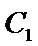的方程；

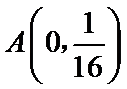
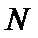
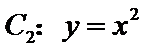
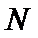
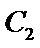
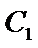
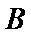
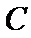
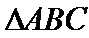
（Ⅱ）设，为抛物线上一动点，过点作抛物线的切线交椭圆于，两点，求面积的最大值．

正确答案

（Ⅰ）

（Ⅱ）

解析

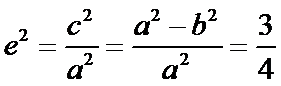
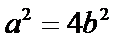
（Ⅰ）因为，所以．

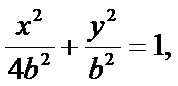
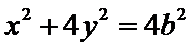
则椭圆方程为即．

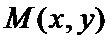
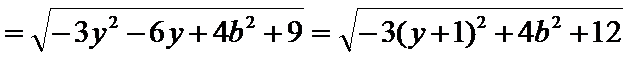
设，则

．

当时，有最大值为．

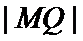
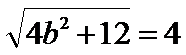
解得，则．

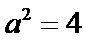
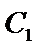
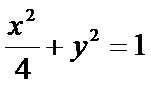
所以椭圆的方程是．

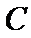
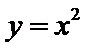
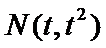
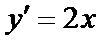
（Ⅱ）设曲线：上的点，因为，

所以直线的方程为：． ①

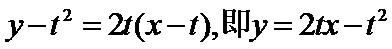
将①代入椭圆方程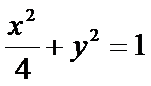中整理，

得．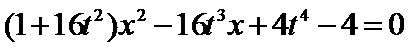

则有．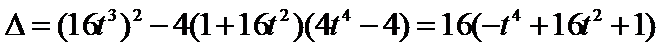

且．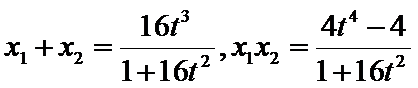

所以

．

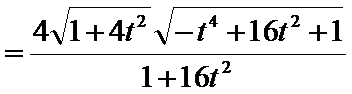
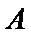
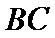
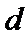
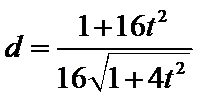
设点到直线的距离为，则．

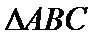
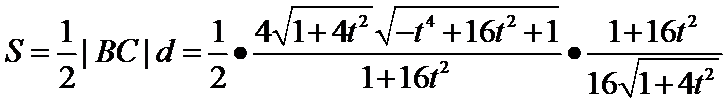
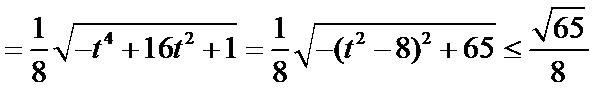
所以的面积．

．

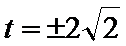
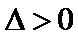
当时取到“=”，经检验此时，满足题意．

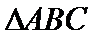
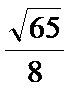
综上，面积的最大值为．

考查方向

本题考查了直线与圆锥曲线的关系，椭圆的标准方程以及二次函数求最值。

解题思路

易错点

第一问未能利用|MQ|最大值求出b;第二问运算量较大，代数式化简容易出错。

知识点

椭圆的定义及标准方程椭圆的几何性质抛物线的标准方程和几何性质圆锥曲线中的范围、最值问题

题型：填空题

分值: 5分

15．展开式中的常数项为，则．

正确答案

解析

考查方向

本题主要考察二项式定理的性质。

解题思路

易错点

二项式定理公式比较复杂，容易记错。

知识点

求二项展开式的指定项或指定项的系数

简答题（综合题）本大题共58分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

17．设为数列的前项和，已知，对任意，都有．

(Ⅰ)求数列的通项公式；

(Ⅱ）若数列的前项和为,求证：．

正确答案

证明，（Ⅰ）因为，

当时，，

两式相减，得，

即，

所以当时，．

所以．

因为，所以．

（Ⅱ）因为，，，

所以．

所以

．

因为，所以．

因为在上是单调递减函数，

所以在上是单调递增函数．

所以当时，取最小值．

所以．

解析

本题属于数列应用中的基本问题，两问难度相当，（I）直接按照步骤来求（II）要裂项相消求和即可．

考查方向

本题考查了数列的相关知识点：

1、利用递推公式推导通项公式；

2、数列中的关系；

3、利用递推公式求解通项公式要单独把n=1拿出来验证；

4、数列中常用的求和方法----裂项法。

解题思路

易错点

知识点

由an与Sn的关系求通项an数列与不等式的综合

题型：简答题

分值: 12分

18．如图，在三棱柱中，侧棱底面，，，分别是线段的中点，过线段的中点作的平行线，分别交，于点，．

（Ⅰ）证明，平面；

（Ⅱ）求二面角的余弦值．

正确答案

（Ⅰ）证明：因为,是的中点,所以,．

因为，分别为，的中点，所以．

所以．

因为平面,平面，所以．

又因为在平面内,且与相交,

所以平面．

（Ⅱ）解法一,连接,过作于,

过作于,连接．

由（Ⅰ）知,平面,

所以平面平面．

所以平面,则．

故为二面角的平面角(设为)．

设,则由,,有,．

又为的中点，则为的中点，所以．

在，，在中，．

从而,．

所以．

因为为锐角，

所以．

故二面角的余弦值为．

解法二,设．如图,过作平行于,以为坐标原点,分别以,的方向为轴,轴,轴的正方向,建立空间直角坐标系(点与点重合)．

则,．

因为为的中点,所以分别为的中点,

故,

所以,,．

设平面的法向量为，

则即故有

从而取,则,

所以是平面的一个法向量．

设平面的法向量为,

则即故有

从而取,则,

所以是平面的一个法向量．

设二面角的平面角为,又为锐角，

则

．

故二面角的余弦值为．

解析

设．如图,过作平行于,以为坐标原点,分别以,的方向为轴,轴,轴的正方向,建立空间直角坐标系(点与点重合)．

则,．

因为为的中点,所以分别为的中点,

故,

所以,,．

设平面的法向量为，

则即故有

从而取,则,

所以是平面的一个法向量．

设平面的法向量为,

则即故有

从而取,则,

所以是平面的一个法向量．

设二面角的平面角为,又为锐角，

则

．

故二面角的余弦值为．

考查方向

本题考查了立体几何的基本问题，分类讨论讨论点大体可以分成以下几类：

1、线面垂直问题；

2、二面角问题。

解题思路

1、选取合适的单位长度，根据图像的框架结构建立合适的直角坐标系。

2、确定问题所需的点的坐标。

易错点

本题如果利用纯几何法，第一问相较容易，但是第二问找二面角难度较大，而且本题建立直角坐标系的垂直的三线是现成的，所以本题建议用空间向量法解决以提高正确率。

知识点

直线与平面垂直的判定与性质线面角和二面角的求法

题型：简答题

分值: 12分

19．计划在某水库建一座至多安装3台发电机的水电站，过去50年的水文资料显示，水库年入流量(年入流量：一年内上游来水与库区降水之和，单位：亿立方米）都在40以上．其中，不足80的年份有10年，不低于80且不超过120的年份有35年，超过120的年份有5年．将年入流量在以上三段的频率作为相应段的概率，并假设各年的年入流量相互独立．

（Ⅰ）求在未来4年中，至多1年的年入流量超过120的概率；

（Ⅱ）水电站希望安装的发电机尽可能运行，但每年发电机最多可运行台数受年入流量限制，并有如下关系；

若某台发电机运行，则该台发电机年利润为5000万元；若某台发电机未运行，则该台发电机年亏损800万元，欲使水电站年总利润的均值达到最大，应安装发电机多少台？

正确答案

（Ⅰ）

（Ⅱ）2

解析

（I）依题意，

，．

由二项分布，在未来4年中至多有1年入流量超过120的概率为：

．

（Ⅱ）记水电站年总利润为（单位：万元），

由于水库年入流量总大于40,所以至少安装1台．

①安装1台发电机的情形：

由于水库年入流量总大于40，所以一台发电机运行的概率为1，

对应的年利润，．

②安装2台发电机的情形：

当时，一台发电机运行，此时，

因此．

当时，两台发电机运行，此时，

因此．

所以的分布列如下：

所以．

③安装3台发电机的情形：

当时，一台发电机运行，此时，

因此．

当时，两台发电机运行，此时，

此时．

当时，三台发电机运行，此时，

因此．

所以的分布列如下：

所以．

综上，欲使水电站年总利润的均值达到最大，应安装2台发电机．

考查方向

本题考查了离散型随机变量的期望与方差，离散型随机变量及其分布列

解题思路

（Ⅰ）先求出年入流量X的概率，根据二项分布，求出未来4年中，至少有1年的年入流量超过120的概率；

（Ⅱ）分三种情况进行讨论，分别求出一台，两台，三台的数学期望，比较即可得到．

易错点

第一问较简单，明确二项分布原理就不易出错，第二问分类出错

知识点

古典概型的概率离散型随机变量及其分布列、均值与方差

题型：简答题

分值: 10分

22．选修4—1：几何证明选讲。

如图，于点，以为直径的圆与交于点．

（Ⅰ）求证：；

（Ⅱ）若，点在线段上移动，,与相交于点，求的最大值．

正确答案

解,（Ⅰ）在中，，于点，

所以，

因为是圆的切线，

由切割线定理得．

所以．

（Ⅱ）因为，所以．

因为线段的长为定值，即需求解线段长度的最小值．

弦中点到圆心的距离最短，此时为的中点，点与点或重合．

因此．

解析

（Ⅰ）在中，，于点，

所以，

因为是圆的切线，

由切割线定理得．

所以．

（Ⅱ）因为，所以．

因为线段的长为定值，即需求解线段长度的最小值．

弦中点到圆心的距离最短，此时为的中点，点与点或重合．

因此． 23. （Ⅰ）曲线：的直角坐标方程为．

曲线与轴交点为．

曲线：的直角坐标方程为．

曲线与轴交点为．

由，曲线与曲线有一个公共点在x轴上，知．

（Ⅱ）当时, 曲线：为圆．

圆心到直线的距离．

所以两点的距离．

考查方向

本题考查了几何选讲部分的直线与圆中的切割线定理、垂径定理以及直角三角形射影定理，高考在22题中的三选一出现。

解题思路

易错点

第一问未能准确读图，找到线段关系;第二问不能充分利用OF⊥NF得到，则无法继续求解。

知识点

圆的切线的判定定理的证明与圆有关的比例线段

题型：简答题

分值: 12分

21．已知函数（为自然对数的底数，为常数）在点处的切线斜率为．

（Ⅰ）求的值及函数的极值；

（Ⅱ）证明：当时，；

（Ⅲ）证明：对任意给定的正数，总存在，使得当，恒有．

正确答案

（Ⅰ）见解析

（Ⅱ）见解析

（Ⅲ）见解析

解析

（Ⅰ）解,由，得．

因为,所以．

所以，．

令,得．

当时, 单调递减；当时, 单调递增．

所以当时, 取得极小值,且极小值为无极大值．

（Ⅱ）证明,令,则．

由（Ⅰ）得,故在R上单调递增．

所以当时，，即．

（Ⅲ）证明一,①若,则．

由（Ⅱ）知，当时，．所以当时, ．

取,当时，恒有．

②若,令,

要使不等式成立，只要成立．

而要使成立，则只要,只要成立．

令,则．

所以当时, 在内单调递增．

取,所以在内单调递增．

又，

易知．

所以．即存在,当时，恒有．

综上，对任意给定的正数，总存在,当时,恒有．

证明二,对任意给定的正数，取，

由（Ⅱ）知，当时，，所以．

当时，．

因此，对任意给定的正数，总存在,当时,恒有．

证明三,首先证明当时，恒有．

令，则．

由（Ⅱ）知，当时，，

从而，在上单调递减。

所以，即．

取，当时，有．

因此，对任意给定的正数，总存在,当时,恒有．

考查方向

本题考查导数与函数极值问题。

解题思路

易错点

第一问建议做出极值表便于观察，防止出错；

第二问忽略证明第一问时得到的结论。

知识点

导数的几何意义导数的运算不等式恒成立问题

理科数学 热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

理科数学热门试卷