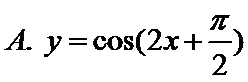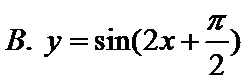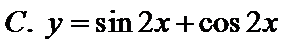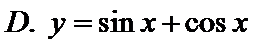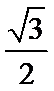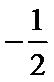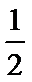- 真题试卷
- 模拟试卷
- 预测试卷
4.下列函数中,最小正周期为且图象关于原点对称的函数是( )
正确答案
解析
对于选项A,因为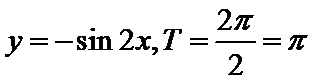
考查方向
解题思路
先将选项化简后利用三角函数的周期和奇偶性判断即可。
易错点
利用诱导公式化简时没有注意奇偶导致出错;不会利用辅助角公式化简C,D选项。
知识点
5.过双曲线

正确答案
解析
双曲线的右焦点为




考查方向
解题思路
先根据双曲线方程求出基本量后,将


易错点
将双曲线中的基本量与椭圆中的混淆导致出错;将
知识点
6.用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有( )A.144个
正确答案
解析
据题意,万位上只能排4、5.若万位



考查方向
解题思路
先根据题意,确定分类的标准,按照万位上的数字分类,然后求出每类的结果后相加即可。
易错点
不确定如何分类导致结果出错;
知识点
8.设a,b都是不等于1的正数,则“
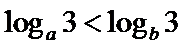
正确答案
解析
若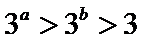
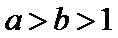
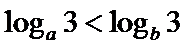
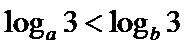
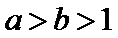
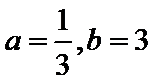
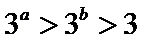
考查方向
解题思路
直接根据充要条件的判断方法判断即可。
易错点
对于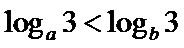
知识点
9.如果函数

正确答案
解析



















考查方向
解题思路
先根据是否是二次函数分类,然后



易错点
1.不能将题中给出的函数正确分类;
分类后想不到利用基本不等式导致没有思路。
知识点
10.设直线l与抛物线

正确答案
解析
不妨设直线




代入


可得


考查方向
解题思路
先设直线方程后代人消元得到判别式






易错点
1.不会转化题中给出的条件这样的直线l恰有4条;
找不到r和t之间的关系导致没有思路。
知识点
1.设集合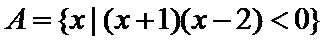
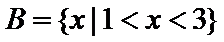
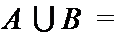
正确答案
解析
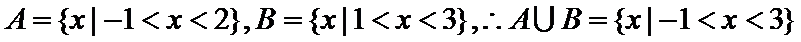
考查方向
解题思路
先解出集合A,后直接在数轴上求解既可。
易错点
不注意数轴导致端点出错或集合A解错。
知识点
2.设i是虚数单位,则复数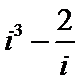
正确答案
解析
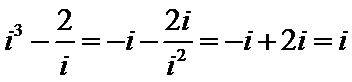
考查方向
解题思路
直接根据复数的运算法则求解既可。
易错点
对于题中的负号处理可能会出错。
知识点
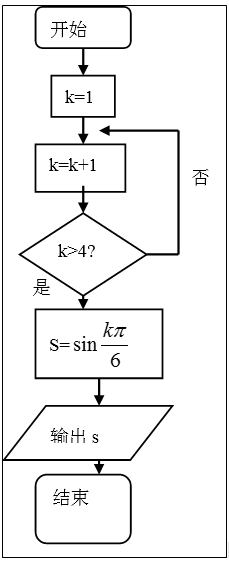
3.执行如图所示的程序框图,输出S的值是( )
正确答案
解析
这是一个循环结构,每次循环的结果依次为:
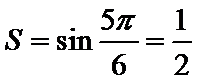
考查方向
解题思路
根据程序框图顺序执行即可得到答案。
易错点
不清楚循环结束的条件导致出错。
知识点
7.设四边形ABCD为平行四边形,




正确答案
解析


考查方向
解题思路
先将所求向量用题中给出的向量表示出来后代人要求的式子化简即可。
易错点
1.不知道如何将题中要求的向量用已知向量表示;
利用向量的法则表示向量时出错。
知识点
一个正方体的平面展开图及该正方体的直观图的示意图如图所示,在正方体中,设


20.请将字母
21.证明:直线
22.求二面角
正确答案
点F、G、H的位置如图所示.
解析
点F、G、H的位置如图所示.
考查方向
解题思路
注意ABCD是底面,将平面展开图还原可得点F、G、H的位置.
易错点
1.将展开图还原出错;
正确答案
详见解析.
解析
连结BD,设O为BD的中点.
因为M、N分别是BC、GH的中点,
所以



所以

所以

从而
又



所以

考查方向
解题思路
根据直线与平面平行的判定定理,应考虑证明MN平行于平面BDH内的一条直线.连结O、M,易得



易错点
找不到与MN平行的直线导致无法证明;
正确答案
解析
连结AC,过M作
在正方形

所以
过P作
所以

从而
所以

设

在

在

所以
即二面角

考查方向
解题思路
要作出二面角

易错点
利用向量法求解运算出错或找不到

如图,A,B,C,D为平面四边形ABCD的四个内角.
23.证明:
24.若
正确答案
详见解析;
解析

考查方向
解题思路
首先切化弦得

易错点
不会转化角之间的关系导致没有思路。
正确答案

解析
由

由(1),有
连结BD,
在

在

所以 
则
于是
连结AC,同理可得

于是
所以

考查方向
解题思路
由题设知,该四边形的两对






易错点
1.第(2)问想不到利用第(1)问的结论;
化简得到
某市A,B两所中学的学生组队参加辩论赛,A中学推荐3名男生,2名女生,B中学推荐了3名男生,4名女生,两校推荐的学生一起参加集训,由于集训后队员的水平相当,从参加集训的男生中随机抽取3人,女生中随机抽取3人组成代表队
18.求A中学至少有1名学生入选代表队的概率.
19.某场比赛前,从代表队的6名队员中随机抽取4人参赛,设X表示参赛的男生人数,求X得分布列和数学期望.
正确答案
A中学至少1名学生入选的概率为
解析
由题意,参加集训的男女生各有6名.
参赛学生全从B中抽取(等价于A中没有学生入选代表队)的概率为
因此,A中学至少1名学生入选的概率为
考查方向
解题思路
.弄清题意后直接利用古典概率的概率公式先求对立事件的概率后即可得到答案;
易错点
对于题意理解有困难,不知道说的是什么导致没有思路。
正确答案
X的分布列为:
X的期望为
解析
根据题意,X的可能取值为1,2,3.



所以X的分布列为:
因此,X的期望为
考查方向
解题思路
直接根据超几何分布求解即可。
易错点
题中的概率错误的理解为是二项分布出错。
如图,椭圆E:







25.求椭圆E的方程;
26.在平面直角坐标系

正确答案

解析
由已知,点
因此,
解得
所以椭圆的方程为
考查方向
解题思路
根据椭圆的对称性,当直线







易错点
不会转化题中给出的条件
正确答案
存在,Q点的坐标为
解析
当直线



如果存在定点Q满足条件,则

所以Q点在y轴上,可设Q点的坐标为
当直线


则
由



所以,若存在不同于点P的定点Q满足条件,则Q点的坐标

下面证明:对任意的直线

当直线
当直线



联立

其判别式
所以,
因此
易知,点B关于y轴对称的点的坐标为
又
所以

所以
故存在与P不同的定点

考查方向
解题思路
先利用










易错点
想不到先解决特色情况再证明一般情况。
设数列



16.求数列
17.记数列


正确答案
解析
由已知

即
从而
又因为

所以

所以,数列
故
考查方向
解题思路
利用





易错点
不会根据Sn=2an-a3求出an=2an-1(n≥2);
正确答案
10.
解析
由(1)得
所以
由

因为
所以
于是,使
考查方向
解题思路
由(1)得



易错点
求前n项和时对于项数出错。
已知函数
27.设
28.证明:存在




正确答案
当






解析
由已知,函数


所以
当


在区

当


解题思路
首先对函数




易错点
不会确定分类的标准导致出错或不分类;
正确答案
详见解析.
解析
由

令
则
故存在

令
由


所以
即
当

由(1)知,函数

故当


当


所以,当

综上所述,存在




考查方向
解题思路
要使得













因为










当



故当







易错点
找不到解决问题的思路导致无法入手。
11.在

正确答案
-40
解析



考查方向
解题思路
直接利用二项式的通项公式即可得到答案。
易错点
不注意要求的是系数还是二项式系数导致出错。
知识点
13.某食品的保鲜时间y(单位:小时)与储存温度x(单位:





正确答案
24
考查方向
易错点
1.没有发现192与48之间的关系导致不会解方程组;
知识点
14.如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ上,E、F分别为AB、BC的中点。设异面直线EM与AF所成的角为

正确答案
解析
建立坐标系如图所示.设








考查方向
解题思路
建立坐标系后直接根据坐标求解即可;
易错点
1.点或向量的坐标写错;
不会利用基本不等式求最值。
知识点
15.已知函数





现有如下命题:
(1)对于任意不相等的实数

(2)对于任意的a及任意不相等的实数

(3)对于任意的a,存在不相等的实数

(4)对于任意的a,存在不相等的实数

其中的真命
正确答案
①④
解析
对于①,因为f '(x)=2xln2>0恒成立,故①正确;
对于②,取a=-8,即g'(x)=2x-8,当x1,x2<4时n<0,②错误;
对于③,令f '(x)=g'(x),即2xln2=2x+a,记h(x)=2xln2-2x,则h'(x)=2x(ln2)2-2,存在












考查方向
解题思路
逐个判断各个选项的正误即可。
易错点
1.不明白题中给出的条件是什么;
对于③④,不知道该如何判断正误。
知识点
12.
正确答案
解析

考查方向
解题思路
先利用诱导公式将

易错点
意识不到15度和75度之间的关系出错或不会利用辅助角公式出错。