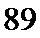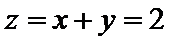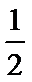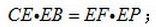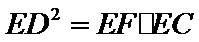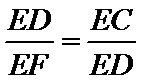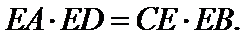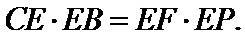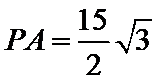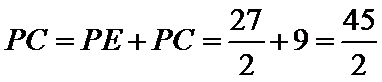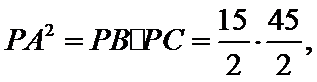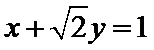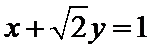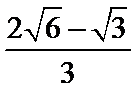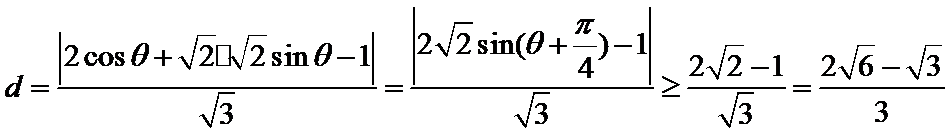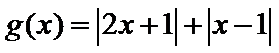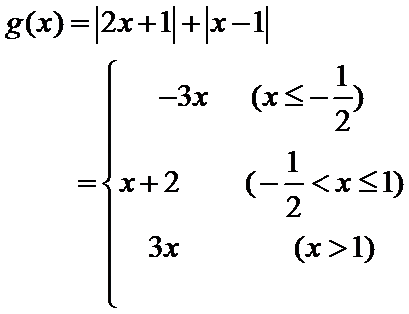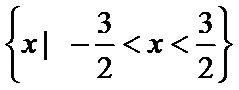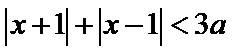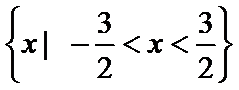- 真题试卷
- 模拟试卷
- 预测试卷
1.已知


正确答案
解析


考查方向
解题思路
求出集合M、N中y的取值范围,再取交集。
易错点
弄错集合M,N的意义,没有注意集合研究的对象。
知识点
2. 在复平面内,复数
正确答案
解析


考查方向
解题思路
本题属于简单题,可使用直接法,
(1)化简原式得到
(2)观察实部和虚部对应的正负
易错点
计算过程易忽略
知识点
5.下列叙述正确的个数是 ( )
①l为直线,α、β为两个不重合的平面,若l⊥β,α⊥β,则l∥α
②若命题
③在△ABC中,“A>B”是“sinA>sinB”的充要条件
④若向量a,b满足a·b<0,则a与b的夹角为钝角
正确答案
解析
对于第一个命题,直线l有可能含于平面α;第二个是对的;第三个也是对的,主要它有一个前提,在△ABC中,这就限制了角A的范围,所以根据正弦定理都可判断。第四个是错的,向量a,b满足a·b<0,有可能它们的夹角是180度,是平角,而不是钝角。
考查方向
解题思路
对各个概念的准确理解是解决这道题的关键,解题思路详见解析。
易错点
空间想象能力不够容易对第一个命题判定不准确,第二个由于对全称命题和特称命题不熟悉也会导致出错,第三个容易对前提条件忽视,第四个对两个向量的夹角为0度容易忽视导致出错。
知识点
6. 一个几何体的三视图如图所示,则这个几何体的表面积为
正确答案
解析
该几何体由底半径为1的半圆锥与底面为边长等于2正方形的四棱锥组成,且高都为
半个圆锥的侧面积
半个圆锥的底面积
四棱锥的侧面积
四棱锥的底面积
所以,整个组合体的表面积为
考查方向
解题思路
先看懂这个三视图所表示的组合体是由哪几部分构成的,然后根据圆锥、四棱锥的表面积公式代入计算即可得到答案。
易错点
看不懂三视图所表示的直观图导致不知道从什么地方入手,对组合体不熟悉导致出错,在计算组合体的体积时,不清楚椎体的表面积公式也会出错。再者就是计算出错。
知识点
8. 已知



正确答案
解析
由余弦定理
则
又因为

即
即
由正弦定理得
即
所以,
考查方向
解题思路
先切化弦、化简向量的数量积,然后根据余弦定理、正弦定理进行化简即可得到答案。
易错点
不懂切化弦导致不知道从什么地方入手,对向量数量积不熟悉导致出错,在余弦定理的反应用时,不清楚余弦定理反过来也会化简。再者就是计算出错。
知识点
9. 若定义在R上的函数f(x)满足f(-x)=f(x), f(2-x)=f(x),且当x∈[0,1]时,其图象是四分之一圆(如图所示),则函数H(x)= |xex|-f(x)在区间
正确答案
解析
f(-x)=f(x), f(2-x)=f(x),所以f(x)是偶函数、周期是2
令
求导得,





根据



考查方向
解题思路
先看懂这个四分之一圆所表示的图像只是函数的一部分构成的,然后根据函数的奇偶性以及周期性即可得到在区间[-3,1]上的f(x)图象。
易错点
看不懂图所表示的四分之一圆导致不知道从什么地方入手,对函数奇偶性周期性不熟悉导致出错,在计算函数的单调性时,不清楚函数的零点定义也会出错。再者就是计算出错。
知识点
3. 设随机变量ξ服从正态分布


正确答案
解析
由正态分布曲线可知,


考查方向
解题思路
根据正态分布曲线可知,数学期望是
易错点
对正态分布曲线不熟悉导致出错;不清楚


知识点
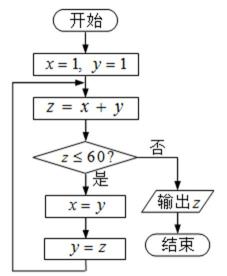
4. 有一个古老的数列,它的意义非同一般,是意大利数学家里昂那多.斐波那契首次提出。现在给出如图所示的程序框图(算法流程图),那么它的输出结果是( )
正确答案
解析
由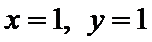
判断z=2满足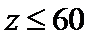
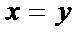
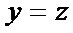
在得到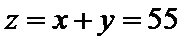
考查方向
解题思路
按照框图中的计算顺序,一步一步计算即可,中间主要就是熟悉当型的循环结构。再者就是这个数列是斐波那契数列,如果看懂框图,对这个数列熟悉的话,直接就可以得出结果。
易错点
对循环结构中的当型循环结构不熟悉导致出错;在斐波那契数列的计算中容易出错。
知识点
7.定义在






正确答案
解析
由






因为对任意的


















若





















考查方向
解题思路
本题属于中等题,可使用数形结合法,
(1)由

(2)由




(3)利用图形可得结论。
易错点
不会利用已知条件求函数的对称轴,不会判断函数的单调性,搞不清充分条件与必要条件。
知识点
10. 在今年的五一期间,某高校4名大学生申请去A,B,C三个旅游景点做志愿者,景区管委会给他们这样安排,每个景点至少分配一人,每人只能到一个景点。在安排的时候。甲要求不去景点A,则不同的安排方案共有( )
正确答案
解析
若甲单独一组,则有
若甲不单独一组,则
所以不同的安排方案共有24种。
考查方向
解题思路
先分类,甲单独一组和甲与另一个人一组,然后在每一类中利用分布计数原理写出组合数。
易错点
分类不清导致出错;分类加法原理和分步计数原理搞错。
知识点
12.已知函数



正确答案
解析





又因为




考查方向
解题思路
利用正弦曲线的对称性,知道





易错点
不会作出分段函数图像,找不到对称关系。
知识点
11. 设双曲线





正确答案
解析
设边长为
由于离心率
所以

而
由于双曲线的离心率e>1,所以

考查方向
解题思路
在三角形中,利用余弦定理,判断边
易错点
此题容易在双曲线的离心率与方程中a、b、c的关系上出错;余弦定理应用时出错;再者就是计算失误
知识点
已知等比数列


17.若


18.若数列




正确答案
解析
解:(Ⅰ)在等比数列


所以,由



在等差数列

所以,
考查方向
解题思路
(1)利用已知条件求出首项与公差,即可求出等差数列的通项公式。
易错点
计算过程易搞错等差数列通项公式。
正确答案
(Ⅱ)
解析
(Ⅱ)若数列


因此有

考查方向
解题思路
用裂项相消法求数列
易错点
不会用裂项相消法求数列的前n项和,计算失误也是出错的一个重要原因。
如图,在直三棱柱



19.当
20.当

所成的角的正弦值为
正确答案
设AB=2,则AB=BC=PA=2
根据题意得:
所以
解析
解:以点B为坐标原点,分别以直线BA、BC、BB1
为x轴、y轴建立空间直角坐标系O-xyz。
设AB=2,则AB=BC=PA=2
根据题意得:
所以
考查方向
解题思路
该题解题关键在于找到所求内容的突破点
(1)确定线线垂直的判定:线面垂直→线线垂直
(2)根据已知条件建立坐标系,并标记所需点的坐标
易错点
本题容易在辅助线建立过程出错,空间直角坐标系建立及其坐标表示出错
正确答案
解析
设AB=2,则
又因为


即
即
考查方向
解题思路
该题解题关键在于找到所求内容的突破点
计算相应面的法向量,并求向量的夹角
易错点
本题容易在辅助线建立过程出错,空间直角坐标系建立及其坐标表示出错
已知









24.求此椭圆的方程;
25.设不过原点O的直线
正确答案
解析
当直线


又

解得

考查方向
解题思路
(1)利用圆锥曲线的定义和性质求解曲线方程
(2)利用离心率求
易错点
本题主要有以下几个错误:1、求措四边形
正确答案
S△OPQ的取值范围为 (0,1).
解析
由题意可设直线l的方程为 y=kx+m (m≠0),P(x1,y1),Q(x2,y2),
由
则△=64 k2b2-16(1+4k2b2)(b2-1)=16(4k2-m2+1)>0,
且

故 y1 y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2.
因为直线OP,PQ,OQ的斜率依次成等差数列,
所以
所以

由于直线OP,OQ的斜率存在,且△>0,得-1<m<1.
设d为点O到直线l的距离,则 S△OPQ=


所以 S△OPQ的取值范围为 (0,1).
考查方向
解题思路
利用直线和圆锥曲线之间的关系,求出韦达定理。利用公式
易错点
本题主要有以下几个错误:1.求△OPQ面积无法确定底和高,2.这里的计算是大问题,经常在计算上出错。
每年四月,很多学校都会组织运动会。在某所大学的运动会中,有一项篮球的投篮比赛。已知某专业的一名同学每次投进篮筐的概率是
21.假设这名同学投篮5次,求有3次连续投进篮筐,另外2次没有投进的概率;
22.假设这名同学投篮5次,求恰有2次投进的概率;
23.假设这名同学投篮3次,每次投进得1分,没有投进得0分,在3次投篮中,若有2次连续投进,而另外1次没有投进,则额外加1分;若3次全投进,则额外加3分,记

正确答案
解析
解:设为事件

=
=
考查方向
解题思路
设出“第
易错点
本小题容易在对互斥事件的判断出错;另一个易错点就是计算。
正确答案
解析
解:设


考查方向
解题思路
(2)分析清楚二项分布即可;
易错点
本小题容易在对二项分布认识不清楚的情况下出错;另一个易错点就是计算。
正确答案
解析
解:由题意可知,
=
所以

考查方向
解题思路
在第一二问的基础上得出

易错点
本小题容易在对分布列认识不清楚的情况下出错;对期望公式不熟悉也是出错的一个原因;另一个易错点就是计算。
请考生在以下三题中任选一题作答,如果多做,则按所做的第一题记分.作答时用2B铅笔在答题卡上把所选题目对应的题号涂黑.
【选修4—1】几何证明选讲(请回答28、29、30题)
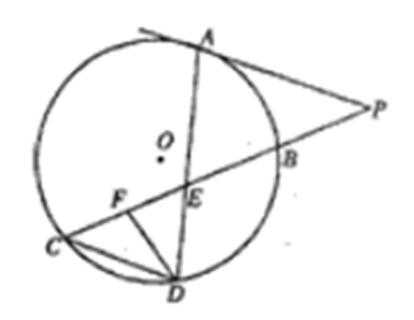
如图:已知PA切圆O于A,PBC是割线,弦CD∥AP,AD交BC于E,F在CE上,且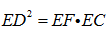
【选修4—4】坐标系与参数方程(请回答31、32题)
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系。已知曲线C1的极坐标方程为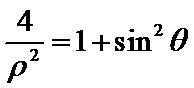
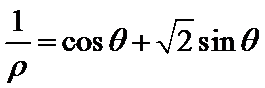
【选修4—5】不等式选讲(请回答33、34题)
已知函数
28.求证:∠EDF=∠P;
29.求证:
30.若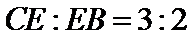
31.写出曲线C1与直线l的直角坐标方程;
32.设Q为曲线C1上一动点,求Q点到直线l距离的最小值。
33.求a的值;
34.解不等式:
正确答案
证明:∵
∴
又∵∠DEF=∠CED
∴△DEF∽△CED
∴∠C=∠EDF 又CD∥AP,
∴∠C=∠P.
∴∠EDF=∠P.
解析
证明:∵
∴
又∵∠DEF=∠CED
∴△DEF∽△CED
∴∠C=∠EDF 又CD∥AP,
∴∠C=∠P.
∴∠EDF=∠P.
考查方向
解题思路
先证明△DEF∽△CED,再根据平行求出∠EDF=∠P.
易错点
切割线定理在应用的时候出错,线段成比例找不对容易出错,相似三角形不写成对应的容易导致比例线段出错。
正确答案
证明:
由(1)得∠EDF=∠P,又∠FED=∠PEA,
∴△FED∽△AEP. ∴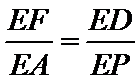
∴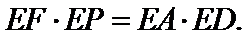
∴
解析
证明:
由(1)得∠EDF=∠P,又∠FED=∠PEA,
∴△FED∽△AEP. ∴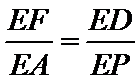
∴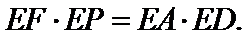
∴
考查方向
解题思路
借助第一问,求得△FED∽△AEP,进而得出成比例线段。
易错点
切割线定理在应用的时候出错,线段成比例找不对容易出错,相似三角形不写成对应的容易导致比例线段出错。
正确答案
解析
证明:
设CE=3k,EB=2k.
∵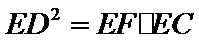
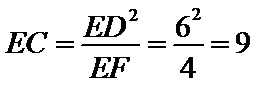
又CE=3k=9, k=3,EB=2k=6.
由(2)得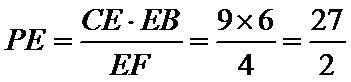
故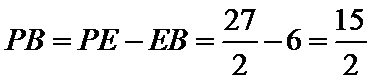
∵
∴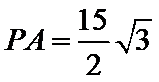
考查方向
解题思路
借助第一二问,根据成比例线段得出结果。
易错点
切割线定理在应用的时候出错,线段成比例找不对容易出错
正确答案
C1的直角坐标方程: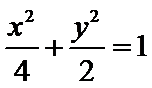
解析
根据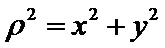
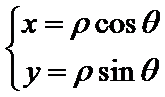
C1的直角坐标方程: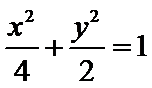
考查方向
解题思路
根据极坐标与直角坐标互化的公式可以直接得到曲线C1与直线l的直角坐标方程;
易错点
极坐标与直角坐标的转化
正确答案
解析
由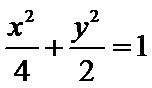
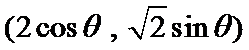
∴点Q到直线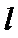
考查方向
解题思路
将曲线C1的直角坐标方程转化为参数方程,代入点Q到直线的距离公式,利用三角恒等变换得到最值。
易错点
点到直线距离公式的应用,计算出错。
正确答案
a=1
解析
可以先不考虑参数a,令
画出图形,即可知道函数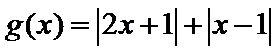
因为函数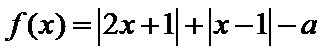
所以a=1
【三级考点】不等式的基本性质,绝对值不等式的解法
考查方向
解题思路
利用零点分段法解绝对值不等式,讨论三种情况。
易错点
在对函数的最小值进行求解时,参数的处理容易出错
正确答案
解析
把a=1代入
利用零点分段法可以得到此不等式的解集是
考查方向
解题思路
利用零点分段法解绝对值不等式,讨论三种情况。
易错点
解决第二问的时候,要注意不等式的最小值。
已知函数
26.若函数
27.证明:
正确答案
实数a的取值范围为
解析
因为
所以
当

当


令
所以

综上所述,实数a的取值范围为
考查方向
解题思路
本题解题思路
(1)第一问借助导数求函数单调性转化为恒成立问题。
(2)利用单调性确定最值求出最值。令



(3)该题的突破点在意恒成立的巧妙转换为最值问题
易错点
本题易错在简单函数符合函数求导,恒成立问题的转化不清,函数分类讨论不清,
正确答案
由(I)知,当a=1时,
得

令
当k为正整数时,令
故
解析
由(I)知,当a=1时,
得

令
当k为正整数时,令
故
考查方向
解题思路
对第二问,本题解题思路,构造函数,利用放缩法巧妙的对不等式进行变形。
易错点
本题易错在简单函数符合函数求导,恒成立问题的转化不清,函数分类讨论不清,
14.我们知道,把所有的正整数按照不同的方式排列,就会出现很多不同的意义。现在把所有正整数按从小到大的顺序排成如图所示的数表,其中第






正确答案
1004
解析
最后一个数是首项为1,等比为2的前n项和,n+1表示行数,当n=10时,即第11行的最后一个数为2047,第11行共有
考查方向
解题思路
最后一个数是首项为1,等比为2的前n项和,n+1表示行数,当n=10时,即第11行的最后一个数为2047,第11行共有
易错点
找不到规律;推理出错,计算错误都是导致出错的原因。
知识点
15. 已知函数



正确答案
解析
点P(2,2),代入直线得2m+2n=1,(

考查方向
解题思路
先求定点坐标,代入直线得2m+2n=1,再利用均值不等式解题
易错点
“1”的应用不灵活
知识点
16. 定义在




②

③

④

则正确命题的序号为 .
正确答案
②③
解析
①因为

②


③因为





④判断不出单调性,所以④不对。
考查方向
解题思路
(1)由










易错点
不会利用已知条件求函数的周期,不会判断函数的对称性
知识点
13. 如果

正确答案
-2
解析




考查方向
解题思路
利用定积分求n=4,再求二项展开式的指定项或指定项的系数
易错点
不会求定积分的值,不会求二项展开式的指定项或指定项的系数。