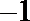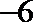- 真题试卷
- 模拟试卷
- 预测试卷
2.下列命题中,真命题是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数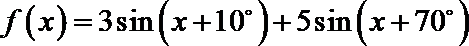
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在直角坐标系中, 如果两点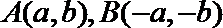
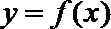

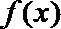
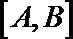
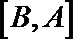
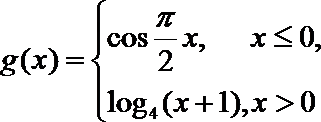
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.将函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设函数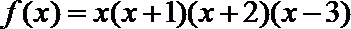
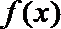
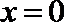
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.若对任意的实数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如果对任意一个三角形,只要它的三边长







正确答案
①③
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数
(1)求

(2)求
正确答案
(1)
∴

(2)函数的周期


解析
解析已在路上飞奔,马上就到!
知识点
19.设



(1)求角
(2)若角




正确答案
(1)因为
所以


所以

(2)由(1)知

设
又
在
即
解得
故
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(1)求函数
(2)讨论函数

正确答案
(1)
∵
∴函数




所以



(2)①当



∴
②当

函数


∴
③当

令



所以当

所以
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(1)求证函数

(2)函数

(3)对

正确答案
(1)
由于



故函数

(2)令


因为函数

有因为当

所以

(3)由(2)可知


所以
记

所以

所以
于是
故对

解析
解析已在路上飞奔,马上就到!
知识点
21. 如下图,某小区准备绿化一块直径为










(1)试用



(2)若

正确答案
(1)在

设正方形的边长为

由

所以
(2)
令


所以

所以函数

因此当


所以当
解析
解析已在路上飞奔,马上就到!