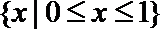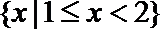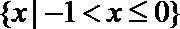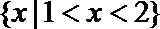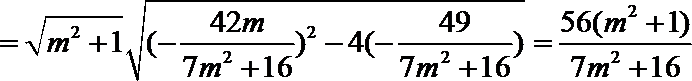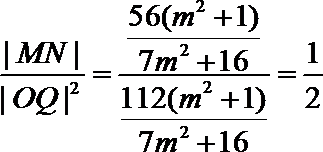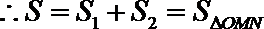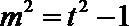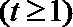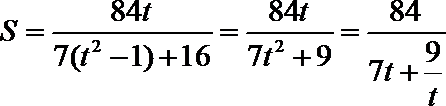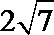- 真题试卷
- 模拟试卷
- 预测试卷
1. 若集合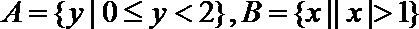
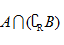
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 如图是一个算法的流程图.若输入


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.某四棱锥的三视图如图所示,记A为此棱锥所有棱的长度的集合,则( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设P是△ABC内任意一点,S△ABC表示△ABC的面积,


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 在平面直角坐标系中,







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知点




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 已知三棱锥





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设












① 

② 

③ 
其中所有正确结论的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 将A,B,C,D,E五种不同的文件放入编号依次为1,2,3,4, 5,6,7的七个抽屉内,每个抽屉至多放一种文件,若文件A、B必须放入相邻的抽屉内,文件C、D也必须放在相邻的抽屉内,则所有不同的放法有 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知关于





正确答案
(-2,-1/2)
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.二项式(1+sinx)n的展开式中,末尾两项的系数之和为7,且系数最大的一项的值为
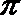
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.对于下列命题:
①函数


②已知



③“


④“

其中所有真命题的序号是 __________。
正确答案
①②④
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知等差数列







(1)求

(2)记数列






正确答案
解:(1)设等差数列



把








(2)由(1)可得
则
=


=

=






解析
解析已在路上飞奔,马上就到!
知识点
18.一个盒子装有六张卡片,上面分别写着如下六个函数:





(Ⅰ)从中任意拿取
(Ⅱ)现从盒子中逐一抽取卡片,且每次取出后均不放回,若取到一张写有偶函数的卡片则停止抽取,否则继续进行,求抽取次数
正确答案
(Ⅰ)





所有的基本事件包括两类:一类为两张卡片上写的函数均为奇函数;
另一类为两张卡片上写的函数为一个是奇函数,
一个为偶函数;故基本事件总数为
满足条件的基本事件为两张卡片上写的函数均为奇函数,故满足条件的基本事件个数为
故所求概率为
(Ⅱ)


故


解析
解析已在路上飞奔,马上就到!
知识点
22.已知曲线










(Ⅰ)求曲线
(Ⅱ)若点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知动圆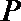
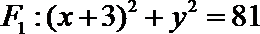
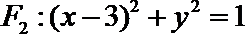
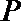
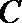
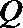
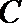
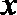
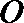
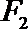
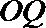
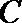
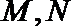
(Ⅰ)求曲线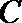
(Ⅱ)试探究
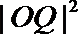
(Ⅲ)记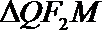
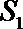
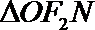
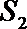
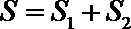
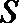
正确答案
解:(I)设圆心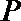
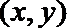
由于动圆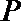
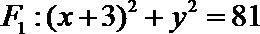
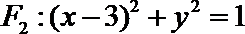
圆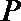
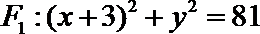
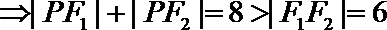
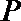
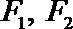
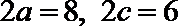
故圆心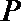
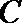
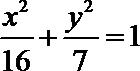
(II)设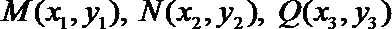
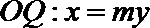
由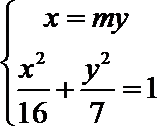
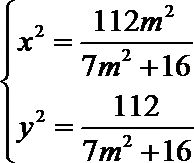
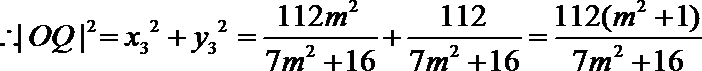
由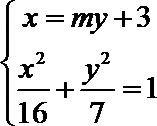

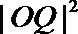
(III)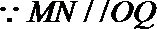
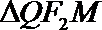
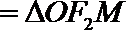
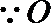
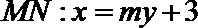
令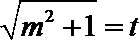
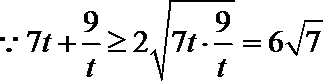
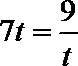
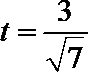
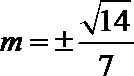
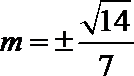
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,在四锥棱






(Ⅰ)求证:

(Ⅱ)求二面角
正确答案
证明:(Ⅰ)连结














(Ⅱ)

















则









由

设平面

由


设平面


由



设二面角



解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数




(Ⅰ)已知


(Ⅱ)若存在


(Ⅲ)设函数










正确答案
解:(Ⅰ)




(Ⅱ)

由

由于



从而

设




从而


所以

(Ⅲ)设











由于

当


当

令



从而

由于


综上可知,

解析
解析已在路上飞奔,马上就到!