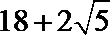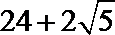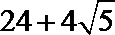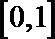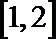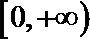- 真题试卷
- 模拟试卷
- 预测试卷
4.要得到函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
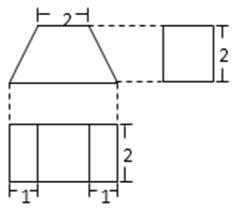
5. 一个几何体的三视图如图所示,则该几何体的表面积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知A,B,C,D,E为抛物线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 已知集合A={1,2,3,4,5},B={(x,y)|x ∈A,y∈A,x+y∈A},则B中所含元素的个数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.下列四种说法中,正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 从1,2,3……20这20个数中任取2个不同的数,则这两个数之和是3的倍数的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.对于函数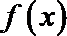
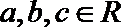
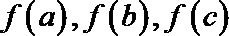
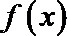

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设





正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
15.对任意两个非零的平面向量











①若

②若

③若

④若


其中正确的命题序号是
正确答案
①③
解析
解析已在路上飞奔,马上就到!
知识点
11. 执行如图所示的程序框图,输出的

正确答案
8194
解析
解析已在路上飞奔,马上就到!
知识点
12.正项数列


正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
14. 





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.前不久,省社科院发布了2013年度“城市居民幸福排行榜”,某市成为本年度城市最“幸福城市”.随后,树德中学校学生会组织部分同学,用“10分制”随机调查“新华西路”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(1)指出这组数据的众数和中位数;
(2)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在


(1)求角B的大小;
(2)设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设各项均为正数的数列





(1)求数列

(2)记数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.在四棱锥








(I)求证:

(II)设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆C:+=1(a>b>0)的离心率e=,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为.
(1)求椭圆C的方程;
(2)过原点且斜率为的直线l,与椭圆交于E,F点,试判断∠EF2F是锐角、直角还是钝角,并写出理由;
(3)P是椭圆上异于A1,A2的任一点,直线PA1,PA2,分别交
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(I)当

(II)当


(III)求证:
正确答案
解析
解析已在路上飞奔,马上就到!