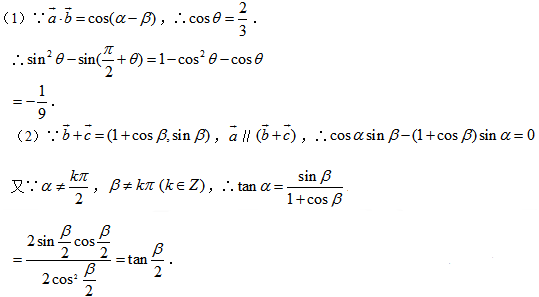- 真题试卷
- 模拟试卷
- 预测试卷
1.若复数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.下列各组向量中:
①e1=(-1,2),e2=(5,7);
②e1=(3,5),e2=(6,10);
③e1=(2,-3),e2=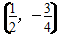
有一组能作为表示它们所在平面内所有向量的基底,这一组是( )(填序号)。
正确答案
①
解析
解析已在路上飞奔,马上就到!
知识点
5.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知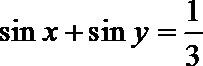
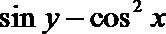
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知命题








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设



正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
2.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知函数


正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
7.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知数列


正确答案
26
解析
解析已在路上飞奔,马上就到!
知识点
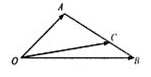
11.如图,已知C为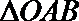
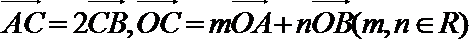
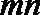
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数

正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
13.已知数列


正确答案
4,5,32
解析
解析已在路上飞奔,马上就到!
知识点
14.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知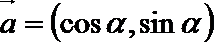

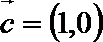
(1)若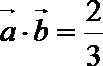
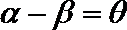

(2)若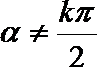

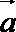
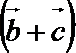
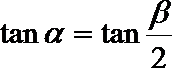
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知二次函数



(1)求
(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点

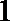
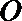
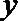
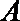
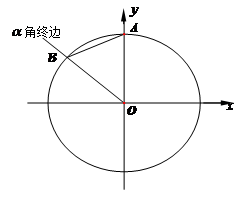
钝角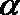
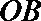
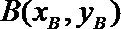
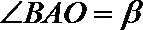
(1)用
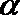
(2)如果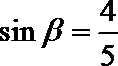
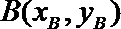
(3)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 如图,在半径为






(1)试写出用


(2)在余下的边角料中在剪出两个圆(如图所示),试问当矩形
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.设函数
(1)设



(2)设



(3)设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知等差数列{an}和正项等比数列{bn},a1=b1=1,a3=b3=2。
(1)求an,bn;
(2)设
(3)设






正确答案
解析
解析已在路上飞奔,马上就到!