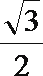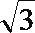- 真题试卷
- 模拟试卷
- 预测试卷
2.若函 数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.阅读下面的程序框图,运行相应的程序,输出的结果为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的外接球的表面积为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设点P(x,y)满足条件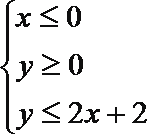

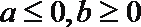
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知在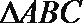

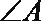
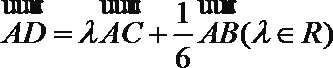
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设直线





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知数列{an}满足3an+1+an=4(n≥1),且a1=9,其前n项之和为Sn。则满足不等式|Sn-n-6|<
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.如图的倒三角形数阵满足:(1)第









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.如果关于




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.定义在





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.动点







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在平面




(Ⅰ)定义横、纵坐标为整数的点为“整点”. 在区域

(Ⅱ)在区域







正确答案
(Ⅰ)依题可知平面区域



∴
(Ⅱ)依题可得,平面区域

平面区域


(设扇形区域中心角为



在区域








∴
∴
(或者:


解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,





(Ⅰ)求证:

(Ⅱ)在棱




正确答案
【法一】(Ⅰ)在线段



则


∴




∴
(Ⅱ)由



过点



则

在






∴
∴



故棱


【法二】建立如图所示的空间直角坐标系,
则





∴





(Ⅰ)∵


∴
(Ⅱ)取


∴



同理,取


∴






又∵

∴



故棱



解析
解析已在路上飞奔,马上就到!
知识点
20.已知中心在原点O,焦点在x轴上,离心率为


(1)求椭圆的方程;
(2)设不过原点O的直线l与该椭圆交于P,Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.
正确答案
(1)由题意可设椭圆方程为
则
所以,椭圆方程为
(2)由题意可知,直线l的斜率存在且不为0,
故可设直线l的方程为y=kx+m(m≠0),P(x1,y1),Q(x2,y2),
由
(1+4k2)x2+8kmx+4(m2﹣1)=0,
则△=64k2b2﹣16(1+4k2b2)(b2﹣1)=16(4k2﹣m2+1)>0,
且

故y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2.
因为直线OP,PQ,OQ的斜率依次成等比数列,[]
所以
即
所以k2=

由于直线OP,OQ的斜率存在,且△>0,得
0<m2<2且m2≠1.
设d为点O到直线l的距离,
则S△OPQ=


所以S△OPQ的取值范围为(0,1).
解析
解析已在路上飞奔,马上就到!
知识点
17.△ABC的三个内角A,B,C依次成等差数列.
(I)若sin2B= sinAsinC,试判断△ABC的形状;
(Ⅱ)若△ABC为钝角三角形,且a>c,试求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设函数
(1)当

(2)令





(3)当



正确答案
所以

当



(3)因为方程
因为


解析
解析已在路上飞奔,马上就到!
知识点
从22、23、24题中任选一题作答。
22.4-1(几何证明选讲)
如图, 






(Ⅰ) 求证: 

(Ⅱ)如果弦






23.选修4-4:坐标系与参数方程
在直角坐标系





(Ⅰ) 写出直线
(Ⅱ) 求 
24.选修4-5:不等式选讲
设不等式


(Ⅰ) 试比较

(Ⅱ) 设



正确答案
22.(Ⅰ)证明:



(Ⅱ)




23.(Ⅰ)

(Ⅱ)



24.(Ⅰ)
(Ⅱ)
解析
解析已在路上飞奔,马上就到!
知识点
13.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.用




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知


正确答案
解析
解析已在路上飞奔,马上就到!