- 真题试卷
- 模拟试卷
- 预测试卷
2.设a∈R,则“a=1”是“直线y=a2x+1与直线y=x-1平行”的( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知复数z满足(3-4i)z=25,则z=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若P(2,-1)为圆(x-1)2+y2=25的弦AB的中点,则直线AB的方程是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如图,一个底面半径为R的圆柱被与其底面所成角为θ(00<θ<900)的平面所截,截面是一个椭圆,当θ为30°时,这个椭圆的离心率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.有红、蓝、黄、绿四种颜色的球各6个,每种颜色的6个球分别标有数字1、2、3、4、5、6,从中任取3个标号不同的球,这3个颜色互不相同且所标数字互不相邻的取法种数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数:
①y=x•sinx;
②y=x•cosx;
③y=x•|cosx|;
④y=x•2x
的图象(部)如图所示,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数f(x)是定义在R上的奇函数,当x<0时,f(x)=ex(x+1),给出下列命题:
①当x>0时,f(x)=ex(1-x);
②f(x)>0的解集为(-1,0)∪(1,+∞);
③函数f(x)有2个零点;
④∀x1,x2∈R,都有|f(x1)-f(x2)|<2;
其中正确命题的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若集合A={x|y=2x},集合
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.下列命题正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设等比数列{an}的前n项和为Sn,若8a2+a5=0,则下列式子中数值不能确定的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知x,y满足
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
13.设(2x+1)5+(x﹣2)4=a0+a1x+a2x2+a3x3+a4x4+a5x5,则a2=_____________。
正确答案
64
解析
解析已在路上飞奔,马上就到!
知识点
14.若方程log3(a-3x)+x-2=0有实根,则实数a的取值范围是________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
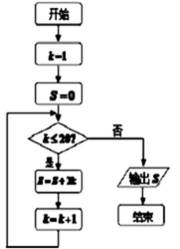
12.如果执行如图所示的程序图(判断条件k≤20?),那么输出的S=_____________。
正确答案
420
解析
解析已在路上飞奔,马上就到!
知识点
15.已知数列{an}是各项均不为0的等差数列,Sn为其前n项和,且满足an2=S2n﹣1(n∈N+).若不等式

正确答案
-21
解析
解析已在路上飞奔,马上就到!
知识点
16.△ABC中角A,B,C的对边分别为a,b,c,且b2+c2﹣a2+bc=0,
(1)求角A的大小;
(2)若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.数列{an}的前n项和为Sn,且an是Sn和1的等差中项,等差数列{bn}满足b1=a1,b4=S3.
(I )求数列{an}、{bn}的通项公式;
(II)设cn=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在四棱锥P﹣ABCD中,底面ABCD是直角梯形,AB∥DC,AB⊥AD,平面PAD⊥平面ABCD,若AB=8,DC=2,AD=6

(1)求证:PO⊥平面ABCD;
(2)设平面PAD与平面PBC所成二面角的大小为θ(0°<θ≤90°),求cosθ的值.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.分别过椭圆E:


(1)求椭圆E的方程;
(2)是否存在定点M,N,使得|PM|+|PN|为定值?若存在,求出M、N点坐标,若不存在,说明理由。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数φ(x)=lnx.
(1)若曲线

(2)求证函数
(3)设m,n∈R+,且m≠n,求证:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某网站用“10分制”调查一社区人们的幸福度.现从调查人群中随机抽取16名,如图所示茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(1)指出这组数据的众数和中位数;
(2)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记ξ表示抽到“极幸福”的人数,求ξ的分布列及数学期望。
正确答案
解析
解析已在路上飞奔,马上就到!