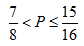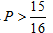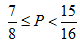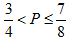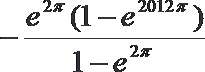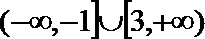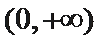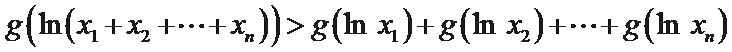- 真题试卷
- 模拟试卷
- 预测试卷
1.已知复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.三棱锥P-ABC中,顶点P在平面ABC上的射影为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知平面向量








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
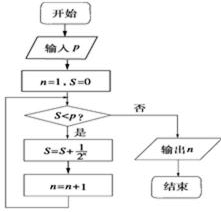
5.执行如图所示的程序框图后,输出的值为4,则P的取值范围是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.双曲线M:


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设函数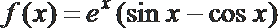
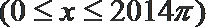
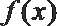
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.甲、乙两位同学,升入高三以来连续五次模拟考试数学单科成绩如下表:
则平均成绩较高与成绩较稳定的分别是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.将一个白球,两个相同的红球,三个相同的黄球摆放成一排。则白球与黄球不相邻的放法有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知f(x)是定义在R上的且以2为周期的偶函数,当0≤x≤1时,f(x)=x2,如果函数g(x)=f(x)-(x+m)有两个零点,则实数m的值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.下图是某四棱锥的三视图,则该几何体的表面积等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知

正确答案
29
解析
解析已在路上飞奔,马上就到!
知识点
15.动点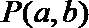
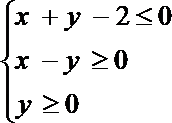
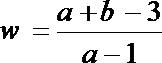
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设等比数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.定义一个对应法则







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.若


(1)求

(2)⊿ABC中a、b、c分别是∠A、∠B、∠C的对边。若

正确答案
解:(1)

由题意,函数



所以,
(2)∵(

∴

⊿ABC中, 则由正弦定理得:



解析
解析已在路上飞奔,马上就到!
知识点
18.今年我校高二理科班学生共有800人参加了数学与语文的学业水平测试,现学校决定利用随机数表法从中抽取100人进行成绩抽样统计,先将800人按001,002,。。。。。800进行编号:
(1)如果从第8行第7列的数开始向右读,请你依次写出最先检测的三个人的编号:(下面摘取了第7行至第9行)
(2)抽出100人的数学与语文的水平测试成绩如下表:
(3)
成绩分为优秀、良好、及格三个等级,横向、纵向分别表示语文成绩与数学成绩,若在该样本中,数学成绩优秀率是30%,求a、b的值;
(3)在语文成绩为及格的学生中,已知


正确答案
解:(1)依题意,最先检测的3个人的编号依次为785,667,199;
(2)由

∵

(3)由题意,知

∴满足条件的
(10,21),(11,20),(12,19),(13,18),(14,17),(15,16),
(16,15),(17,14),(18,13),(19,12),(20,11),(21,10),
(22,9),(23,8)共14组,且每组出现的可能性相同.

解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,五面体





(Ⅰ)




(Ⅱ)当


正确答案
解:(Ⅰ)当



证明:连结


∵ 四边形
∴




∵




(Ⅱ)建立空间直角坐标系
则




所以

设


令


而平面

所以

解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆



(1)求椭圆的离心率
(2)求直线AB的斜率;
(3)设点C与点A关于坐标原点对称,直线



正确答案
解: (1)解:由


整理得

(2)解:由(1)知,
设直线AB的方程为
由已知设

消去y整理,得
依题意,

有题设知,点B为线段AE的中点,所以
解得
将结果代入韦达定理中解得
(3)由(2)知,

得A


直线l与x轴的交点

直线


由



同理可得
解析
解析已在路上飞奔,马上就到!
知识点
22.从22-24题中选择一道做。
22.选修4-1:几何证明选讲
如图,直线








(1)求证:直线

(2)若



23.选修4-4:坐标系与参数方程
已知在直角坐标系






(1)以原点为极点、



(2)在(1)的条件下,设直线



24.选修4-5,不等式选讲
在平面直角坐标系中,定义点




(1)若

(2)当


正确答案



(2)
又







设
23.解:(1)圆锥曲线


所以普通方程为



(2)
24. 解:(1)由定义得

两边平方得

(2)当


法一:函数 令
所以


法二:三角不等式性质
因为


解析
解析已在路上飞奔,马上就到!
知识点
21.对于函数f(x)(x∈D),若x∈D时,恒有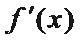
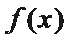
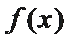
(Ⅰ)当函数f(x)=m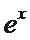
(Ⅱ)若函数g(x)为(0,+∞)上的J函数,试比较g(a)与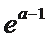
正确答案
解:(Ⅰ)由
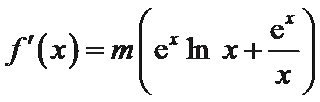
因为函数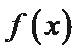
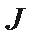
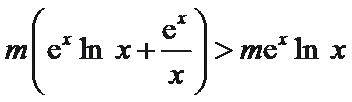
即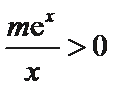
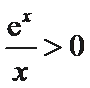
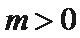
即
(Ⅱ)①构造函数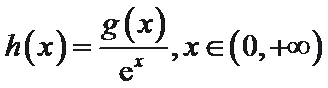
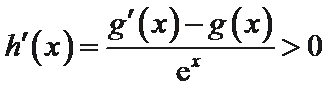
可得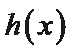
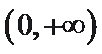
当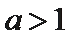
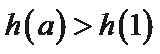
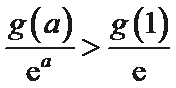
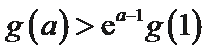
当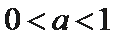
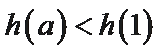
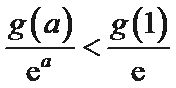
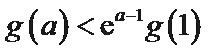
当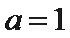
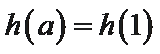
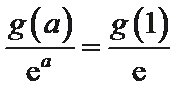
②因为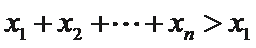
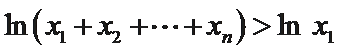
由①可知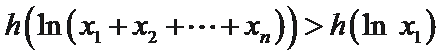

整理得
同理可得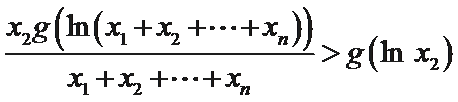
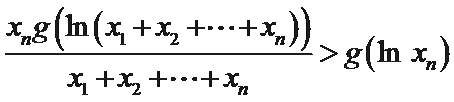
把上面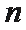
可得
解析
解析已在路上飞奔,马上就到!