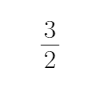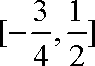- 真题试卷
- 模拟试卷
- 预测试卷
5.设函数f(x)=cos(2x+φ),则“f(x)为奇函数”是“φ=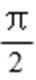
正确答案
必要不充分
解析
略。
知识点
8.设等差数列{an}的前n项和为Sn,若S4≥10,S5≤15,则a4的最大值为________.
正确答案
4
解析
设公差为d,则
即
知识点
9.已知函数y=sinωx(ω>0)在区间[0,
取值集合为()
正确答案
解析





知识点
1.集合M={x|lgx>0},N={x|x2≤4},则M∩N=________.
正确答案
(1,2]
解析
∵M=(1,+∞),N=[-2,2],∴M∩N=(1,2].
知识点
2.已知复数
正确答案
四
解析


知识点
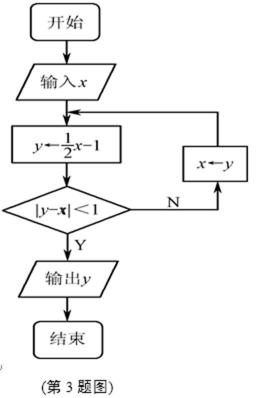
3.如图是一个算法的流程图,若输入x的值为2,则输出y的值是________.
正确答案
-
解析
略。
知识点
7.与正方体各面都相切的球,它的表面积与正方体表面积之比为________.
正确答案
π:6
解析
正方体的棱长与球的直径相等.
知识点
4.某班全体学生参加口语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是________.
正确答案
50
解析
由频率分布直方图,低于60分的频率为(0.01+0.005)×20=0.3.所以该班学生人数为
知识点
10.在




正确答案
4
解析
考查正(余)弦定理及三角形面积公式,基本不等式等知识。
知识点
6.在一个袋子中装有分别标注数字1,2,3,4,5的5个小球,这些小球除标注数字外完全相同.现从中随机取2个小球,则取出的小球标注的数字之和为3或6的概率是__________.
正确答案
解析
基本事件为(1,2)(1,3)(1,4)(1,5)(2,3)(2,4)(2,5)(3,4)(3,5)(4,5),其中和为3或6的有3个,因而有P=
知识点
11.在平面直角坐标系







正确答案
2
解析
即:









知识点
12.若关于x的方程
正确答案
6
解析
两个函数的图象均关于点(2,0)对称.
知识点
14.若实数x,y满足
正确答案
{0}
解析
令

知识点
13.已知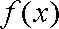
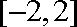
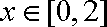
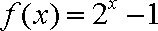
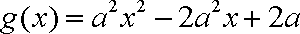
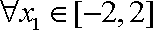
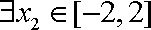
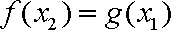
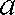
正确答案
解析
由已知得,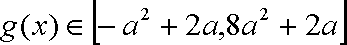
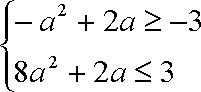
知识点
16.如图,在三棱柱





(1)求证:平面

(2)求证:

正确答案
见解析。
解析
(1)证明:在
在



又点


又








(2)证明:连接
由题意知,点



又





知识点
15.在平面直角坐标系








(1)求函数
(2)设






正确答案
见解析。
解析
(1)由题意,得
所以

因为


(2)因为


在


解得

知识点
17.一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C、D在半圆上),设∠BOC=θ,木梁的体积为V(m3),表面积为S(m2).
(1)求V关于θ的函数表达式;
(2)求体积V的最大值;
(3)当木梁的体积V最大时,其表面积S是否也最大?请说明理由.
正确答案
见解析。
解析
(1)梯形ABCD的面积
SABCD=
体积V(θ)=10(sinθcosθ+sinθ),
(2)V′(θ)=10(2cos2θ+cosθ-1)
=10(2cosθ-1)(cosθ+1).
令V′(θ)=0,得cosθ=
∵


当

当

∴当θ=

(3)木梁的侧面积
S侧=(AB+2BC+CD)·10=20

S=2SABCD+S侧=2(sinθcosθ+sinθ)+20(cosθ+2sin

设g(θ)=cosθ+2sin

∵g(θ)=-2sin2

∴当sin


又由(2)知θ=
∴θ=
综上,当木梁的体积V最大时,其表面积S也最大.
知识点
19.设函数
(1)当

(2)当

(3)若对任意



正确答案
见解析。
解析
(1)函数的定义域为







(2)
当


当





当





综上,当












(3)由(Ⅱ)知,当









知识点
18.如图,在平面直角坐标系





(1)求椭圆
(2)过点



①若直线


②若


是否为定值?若是,请给予证明;若不是,请说明理由.
正确答案
见解析。
解析
(1)由


又椭圆过点


(2)①记




又由




所以


所以圆T的半径为
故

(说明:该圆的一般式方程为
②设直线





直线





所以

又
=

知识点
20.已知数列{


(1)求
(2)证明:

(3)设

正确答案
见解析。
解析
(1)
∵

(2)∵

∴数列{
∴

(3)
∴
∴
由条件可知

a=1时,
a<l时,对称轴


∴

综上知:a≤1时,