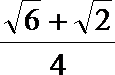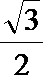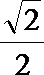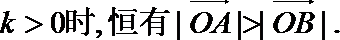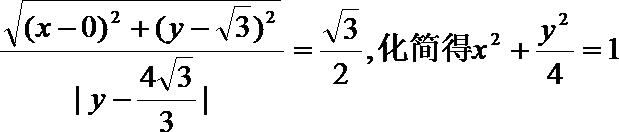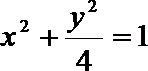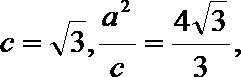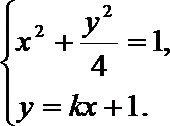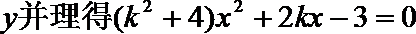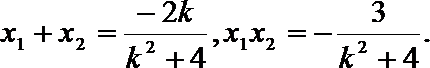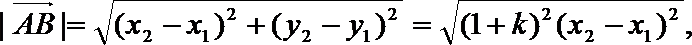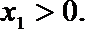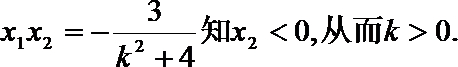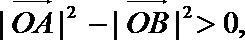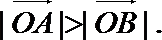理科数学兰州市2010年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

2．函数的最大值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

3．已知函数的导函数，命题处取得极值，则的（）

A充分不必要条件

B必要不充分条件

C充要条件

D既不充分又不必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：单选题

分值: 5分

4．已知复数有（）

A第一象限

B第二象限

C第三象限

D第四象限

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复数的代数表示法及其几何意义复数代数形式的乘除运算

题型：单选题

分值: 5分

5．设随机变量，则的值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

收集数据的方法

题型：单选题

分值: 5分

6．下列结论正确的是（）

A当

B当

C当的最小值是2

D当无最大值

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：单选题

分值: 5分

1．已知集合为（）

A{1，2，3，4}

B{1，3，4，5}

C{2，3，4，5}

D{1，2，3，4，5}

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：单选题

分值: 5分

9．在等差数列等于（）

A20

B100

C25

D50

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：单选题

分值: 5分

10．已知直线与两坐标轴分别相交于A、B两点，圆C的圆心的坐标原点，且与线段AB有两个不同交点，则圆C的半径的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线的倾斜角与斜率

题型：单选题

分值: 5分

8．已知设的图象是（）

A过原点的一条直线

B不过原点的一条直线

C对称轴为轴的抛物线

D对称轴不是轴的抛物线

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

分值: 5分

11．从数字0，1，2，3，5，7，8，11中任取3个分别作为中的A，B，C（A，B，C互不相等）的值，所得直线恰好经过原点的概率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：单选题

分值: 5分

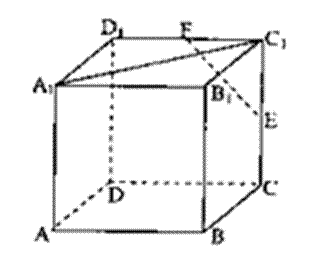
7．在正方体ABCD—A1B1C1D1中，E、F分别是棱CC1与D1C1的中点，则直线EF与A1C1所成角正弦值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

棱柱的结构特征异面直线及其所成的角

题型：单选题

分值: 5分

12．已知定直线与平面α成45°，点P是面α内的一动点，且点P到直线的距离为2，则动点Ｐ的轨迹的离心率是（　　）

C１

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

线面角和二面角的求法椭圆的几何性质

填空题本大题共4小题，每小题5分，共20分。把答案填写在题中横线上。

题型：填空题

分值: 5分

13．已知曲线在点（1,0）处的切线与直线平行，则 ______。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

定义法求轨迹方程

题型：填空题

分值: 5分

14．若的展开式中，只有第5项系数最大，则的展开式中的系数为______。（用数字作答）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：填空题

分值: 5分

16．设，，且，则 _______。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 5分

15．已知点P、Q是内的点，O为坐标原点，则的取值范围是______。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

简答题（综合题）本大题共70分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

18．2008年北京奥运会志愿者中有这样一组志愿者：有几个人通晓英语，还有几个人通晓俄语，剩下的人通晓法语，已知从中任抽一人是通晓英语的人的概率为，是通晓俄语的人数的概率为，是通晓法语的人的概率为，且通晓法语的人数不超过3人。现从这组志愿者中选出通晓英语、俄语和法语的志愿者各1名。

（I）求这组志愿者的人数；

（II）若A通晓英语，求A被选中的概率；

（III）若B通晓俄语，C通晓法语，求B和C不全被选中的概率。

正确答案

（I）设通晓英语的有人，

且

则依题意有：

所以，这组志愿者有人。

（II）所有可能的选法有种

A被选中的选法有种

A被选中的概率为

（III）用N表示事件“B，C不全被选中”，则表示事件“B，C全被选中”

则

所以B和C不全被选中的概率为

说明：其他解法请酌情给分。

解析

解析已在路上飞奔，马上就到！

知识点

随机事件的关系

题型：简答题

分值: 10分

17．已知函数的最小正周期为

（I）求的值；

（II）在角A、B、C的对边分别是求函数的取值范围。

正确答案

（I）

（II）

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 12分

20．已知数列的各项均为正数，其且为等比数列，且是公比为64的等比数列。

（I）求的通项公式；

（II）求证：

正确答案

解：（I）依题意有： ①

所以当 ②

①-②得：化简得：

；

所以数列是以2为公差的等差数列。

故

设

是公比为64的等比数列

（II）

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：简答题

分值: 12分

19．如图，在三棱锥P—ABC中，PA=2，AB=AC=4，点D、E、F分别为BC、AB、AC的中点。

（I）求证：平面PAD；

（II）求点A到平面PEF的距离；

（III）求二面角E—PF—A的大小。

正确答案

解法一：

（I），

AD为PD在平面ABC内的射影。

又点E、F分别为AB、AC的中点，

在中，由于AB=AC，故

，平面PAD

（II）设EF与AD相交于点G，连接PG。

平面PAD，dm PAD,交线为PG，

过A做AO平面PEF，则O在PG上，

所以线段AO的长为点A到平面PEF的距离

在

即点A到平面PEF的距离为

说明：该问还可以用等体积转化法求解，请根据解答给分。

（III）

平面PAC。

过A做，垂足为H，连接EH。

则

所以为二面角E—PF—A的一个平面角。

在

即二面角E—PF—A的正切值为

解法二：

AB、AC、AP两两垂直，建立如图所示空间直角坐标系，

则A（0，0，0），E（2，0，0），D（2，2，0），F（0，2，0），P（0，0，2）

（I）

且

平面PAD

（II）为平面PEF的一个法向量，

则

令

故点A到平面PEF的距离为：

所以点A到平面PEF的距离为

（III）依题意为平面PAF的一个法向量，

设二面角E—PF—A的大小为（由图知为锐角）

则，

即二面角E—PF—A的大小

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

分值: 12分

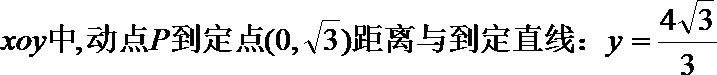
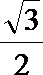
21．在平面直角坐标系的距离之比为。设动点P的轨迹为C。

（I）写出C的方程；

（II）设直线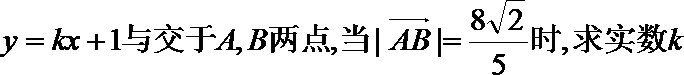的值。

（III）若点A在第一象限，证明：当

正确答案

解：（I）设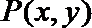，则依题意有：

故曲线C的方程为

注：若直接用

得出，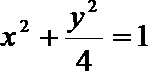

（II）设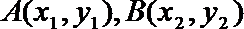，其坐标满足

消去

故

而

化简整理得

解得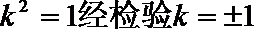：时方程※的△>0

（III）

因为A在第一象限，故

由

故

即在题设条件下，恒有

解析

解析已在路上飞奔，马上就到！

知识点

定义法求轨迹方程

题型：简答题

分值: 12分

22．已知函数

（I）若函数的值；

（II）设的取值范围。

正确答案

解：（I）

处的切线互相平行

；

（II）

令

当

是单调增函数。

恒成立，

值满足下列不等式组

①，或②

不等式组①的解集为空集，解不等式组②得

综上所述，满足条件的

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷