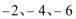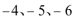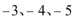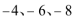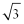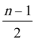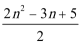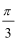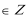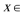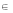- 真题试卷
- 模拟试卷
- 预测试卷
2.“

正确答案
解析
2a>2b⇒a>b,
当a<0或b<0时,
不能得到Ina>Inb,
反之由Ina>Inb即:a>b>0
可得2a>2b成立,
所以2a>2b”是“Ina>Inb”的必要不充分条件
知识点
5.设函数
正确答案
解析
∵f(x)=sinxcos2x,
∴f(-


∴函数f(x)=sinxcos2x图象不关于x=-
∵f(-x)=sin(-x)cos2(-x)=-sinxcos2x=-f(x),
∴f(x)=sinxcos2x为奇函数,不是偶函数,
故不关于直线x=0对称,排除B;
又f(


故函数f(x)=sinxcos2x图象不关于x=
又f(π-x)=sin(π-x)cos2(π-x)=sinxcos2x=f(x)
∴f(x)关于直线x=
知识点
7.要得到一个奇函数,只需将函数
正确答案
解析
f(x)=sin2x-

根据左加右减的原则,只要将f(x)=sin2x-

即可得到函数y=2sin2x的图象,显然函数y=2sin2x为奇函数,
故要得到一个奇函数,只需将函数f(x)=sin2x-

知识点
8.定义在R上的偶函数满足

正确答案
解析
由f(x)满足
由f(x)是定义在R上的偶函数,则f(-x)=f(x)
即有f(x+3)=f(x),则f(x)是以3为周期的函数,
由f(-1)=1,f(0)=-2,即f(2)=1,f(3)=-2,
由f(4)=f(-1)=1,即有f(1)=1.
则f(1)+f(2)+f(3)+…+f(2014)=(1+1-2)+…+f(1)=0×671+1=1.
知识点
1.集合
正确答案
解析
∵A={y∈R|y=2x}={y∈R|y>0},
∴CRA={y∈R|y≤0},
又B={-1,0,1},
∴(CRA)∩B={-1,0}.
知识点
3.已知

正确答案
解析
把sina+cosa=
两边平方得:1+2sinαcosα=
即1+sin2α= 
解得sin2α=-
又sina+cosa=


解得:sin(α+


得到:0<α+



解得

所以2α∈(

则cos2α=-

知识点
4.已知函数


正确答案
解析
因为函数f(x+1)为偶函数,则其图象关于y轴对称,
而函数f(x)的图象是把函数f(x+1)的图象向右平移1个单位得到的,
所以函数f(x)的图象关于直线x=1对称.
又函数f(x)的定义域为(3-2a,a+1),
所以(3-2a)+(a+1)=2,解得:a=2.
知识点
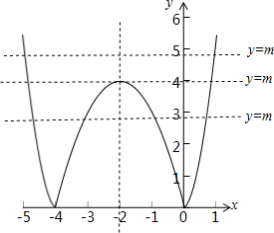
6.若方程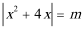
正确答案
解析
函数y=|x2+4x|由函数y=x2+4x的图象纵向对折变换所得:
如下图所示:
由图可得:函数y=|x2+4x|的图象关于直线x=-2对称,
则方程|x2+4x|=m的实根也关于直线x=-2对称,
当m<0时,方程|x2+4x|=m无实根,
当m=0或m>4时,方程|x2+4x|=m有两个实根,它们的和为-4,
当0<m<4时,方程|x2+4x|=m有四个实根,它们的和为-8,
当m=4时,方程|x2+4x|=m有三个实根,它们的和为-6,
知识点
9.在

正确答案
解析
∵sin(A-B)=1+2cos(B+C)sin(A+C),
∴sin(A-B)=1-2cosAsinB,
∴sinAcosB-cosAsinB=1-2cosAsinB,
∴sinAcosB+cosAsinB=1,
∴sin(A+B)=1,
∴A+B=90°,
∴△ABC是直角三角形.
知识点
10.函数
①
②
③函数

④方程
上述关于函数
正确答案
解析
∵函数f(x)的最小值为|AB|=
∴函数的值域[
由函数的值域知,函数图象不可能为中心对称图形,故①错误;
又∵直线AB与x轴交点的横坐标为


∴函数的图象关于直线x=
令t=f(x),由f(t)=1+
由函数的值域可知不成立,∴方程无解,故④错误,
知识点
11.定积分
正确答案
e
解析


知识点
13.函数

正确答案
(
解析
∵函数f(x)=xsinx+cosx+x2,
满足f(-x)=-xsin(-x)+cos(-x)+(-x)2=xsinx+cosx+x2=f(x),
故函数f(x)为偶函数.
由于f′(x)=sinx+xcosx-sinx+2x=x(2+cosx),
当x>0时,f′(x)>0,故函数在(0,+∞)上是增函数,
当x<0时,f′(x)<0,故函数在(-∞,0)上是减函数.
不等式f(lnx)<f(1)等价于-1<lnx<1,∴
知识点
14.已知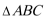
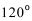
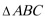
正确答案
15
解析
设三角形的三边分别为x-4,x,x+4,
则cos120°= 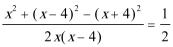
化简得:x-16=4-x,解得x=10,
所以三角形的三边分别为:6,10,14
则△ABC的面积S=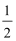
知识点
15.设函数
①对任意的
②对任意的
③对任意的
④对任意的

其中正确的是______________________(填写序号)
正确答案
②
解析
:∵f(x)=lnx是(0,+∞)上的增函数,
∴对于①由f(


∵
故f(

对于②③,不妨设x1<x2则有f(x1)<f(x2),
故由增函数的定义得f(x1)-f(x2)<x2-x1 故②正确,
由不等式的性质得x1f(x1)<x2f(x2),故③错误;
对于④令e=x1<x2=e2,得

∵x0∈(x1,x2),
∴f(x0)>f(x1)=1,
不满足f(x0)≤
知识点
12.如果

正确答案
-
解析
∵f(tanx)=sin2x-5sinx•cosx= 

∴f(x)= 

知识点
17.设命题p:函数





正确答案
p为真命题




q为真命题
由题意p和q有且只有一个是真命题
P真q假
综上所述:
解析
解析已在路上飞奔!
知识点
19.已知数列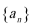
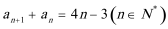
(1)若数列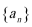
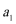
(2) 当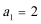
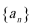
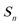
正确答案
(1)若数列{an}是等差数列,
则an=a1+(n-1)d,an+1=a1+nd.
由an+1+an=4n-3,
得(a1+nd)+[a1+(n-1)d]=4n-3,
即2d=4,2a1-d=-3,
解得,d=2,a1=-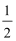
(2)①当n为奇数时,
Sn=a1+a2+a3+…+a_
=a1+(a2+a3)+(a4+a5)+…+(an-1+an)
=2+4[2+4+…+(n-1)]-3×
=
②当n为偶数时,
Sn=a1+a2+a3+…+an
=(a1+a2)+(a3+a4)+…+(an-1+an)
=1+9+…+(4n-7)
=
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数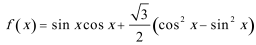
(1)求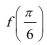
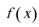
(2)求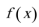
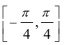
正确答案
(1)f(x)= 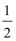
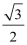
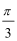
则f(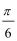
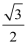
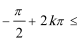
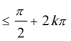
单调递增区间[-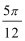
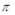
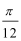
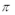
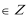
(2)由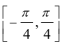
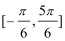
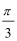
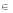
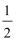
所以最大值为1,最小值为-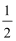
解析
解析已在路上飞奔,马上就到!
知识点
18.在


(1)若


(2)若
正确答案
(1)S△ABC=
由余弦定理得4=a²+b²-2ab×
a=b=2
(2)sinC+sin(B-A)
=2sin2Asin[π-(A+B)]+sin(B-A)
=2sin2Asin(A+B)+sin(B-A)
=2sin2A
sinAcosB+cosAsinB+sinBcosA-cosBsinA=
2sin2A2sinBcosA=2sinAcosAcosA(sinA-sinB)=0
当cosA=0,即A=90°时
B=180°-90°-60°=30°
由正弦定理
得 a=
S=1/2absinC=2√3/3
当sinA=sinB时A=B或A=π-B(舍去)
则A=B=60°
△ABC是等边三角形
a=b=c=2,S=
解析
解析已在路上飞奔!
知识点
20.已知函数



(1)求
(2)对任意的

正确答案
(1)∵f(x)关于y轴对称,
∴f(x)为偶函数,即f(x)=f(-x),
∴a(-x)4+b(-x)3+c(-x)2+d(-x)+e
=ax4+bx3+ax2+dx+e
得b=d=0,
图象过A(0,-1)得e=-1,
∴f(x)=ax4+cx2-1又f(x)在x=

∴f′(


解得a=-2,c=3,
∴f(x)=-2x4+3x2-1;
(2)∵f(x)≤t(x2+1),
∴t≥
=7-[2(x2+1)+ 
∵7-[2(x2+1)+ 

当且仅当2(x2+1)=
即x2=
∴t的取值范围为[7-4
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(1)求实数
(2)证明:
正确答案
(1)解:∵f(x)=
∴f′(x)=2x2+2x+a,
由题意知方程2x2+2x+a=0在(-1,0)上有两不等实根,
设g(x)=2x2+2x+a,
其图象的对称轴为直线x=-
故有
解得0<a<
(2)证明:由题意知x2是方程2x2+2x+a=0的大根,
从而x2∈(-
由于0<a<
∴ax2>
∴f(x2)=


设h(x)=


h′(x)=2(x+

∴h(x)在(-
∴h(x)>h(-
即f(x2)>
解析
解析已在路上飞奔,马上就到!