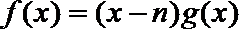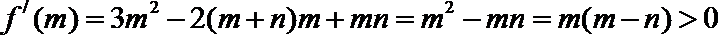- 真题试卷
- 模拟试卷
- 预测试卷
1. 若集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.下列四种说法中,错误的个数是( )
①

②命题“存在

③函数

④已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.“

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.曲线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在边长为1的正三角形


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.函数










正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
15.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在平面直角坐标系

(1)求以线段
(2)设实数


正确答案
(1)因为
则
以线段

(2) 因为
所以

解析
解析已在路上飞奔,马上就到!
知识点
18. 已知










正确答案
若

即


若



若“





(1) 若


(2) 若


综上:

解析
解析已在路上飞奔,马上就到!
知识点
20. 设函数
(1)求函数
(2)若


正确答案
(1)




(2)略
解析
解析已在路上飞奔,马上就到!
知识点
19. 设函数


(1)求
(2)在




正确答案
(1)因为
所以最小正周期是
(2)由

又由余弦定理得,

解①②得


解析
解析已在路上飞奔,马上就到!
知识点
21. 在


(1)判断
(2)若

正确答案
(1)由


所以
因为


所以

三角形为等腰三角形
(2)若


解析
解析已在路上飞奔,马上就到!
知识点
22. 抛物线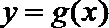
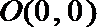
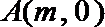
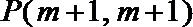
其中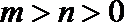
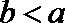
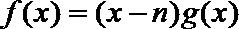

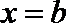
(1)用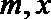
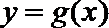
(2) 比较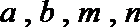
(3)若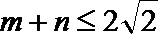
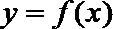
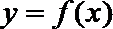
正确答案
(1)由抛物线经过点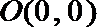
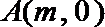
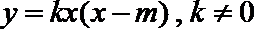
又抛物线过点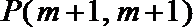
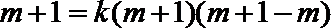
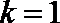
所以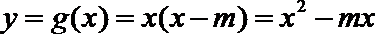
(2)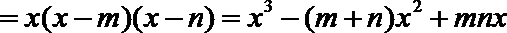
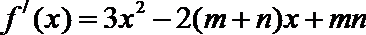
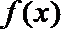

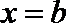
故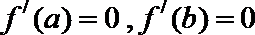
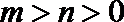
又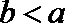
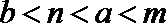
(3)设切点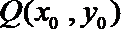
又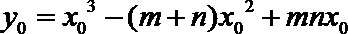
又切线过原点,故
所以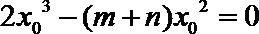
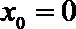
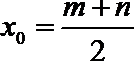
两条切线的斜率为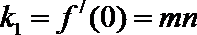
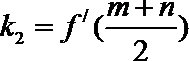
由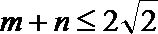
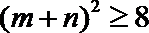
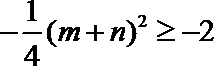
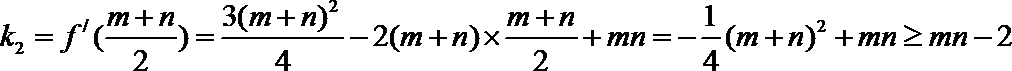
所以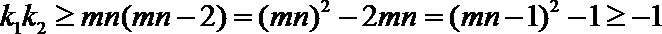
又两条切线垂直,故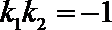
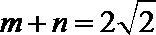
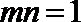
所以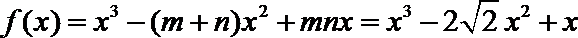
解析
解析已在路上飞奔,马上就到!