- 真题试卷
- 模拟试卷
- 预测试卷
11.已知存在实数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知





正确答案
略
解析
解析已在路上飞奔,马上就到!
知识点
5.底面边长为2m,高为1m的正三棱锥的全面积为( )m2
正确答案

解析
解析已在路上飞奔,马上就到!
知识点
7.已知命题








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知

①
②
③若
④
⑤若
正确答案
①④⑤
解析
解析已在路上飞奔,马上就到!
知识点
4.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设x∈

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设函数










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知O为



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设复数



正确答案
i
解析
解析已在路上飞奔,马上就到!
知识点
13.设









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.定义在D上的函数






(1) 当




(2) 若函数

正确答案
略
解析
解析已在路上飞奔,马上就到!
知识点
23. 已知四棱锥







(1)求异面直线

(2)若

(3)是否存在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.△ABC的外接圆半径为1,角A,B,C的对边分别为a,b,c。向量





(1)求
(2)若实数x满足abx=a+b,试确定x的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.如图,直三棱柱









(1)求证:

(2)设点




正确答案
略
解析
解析已在路上飞奔,马上就到!
知识点
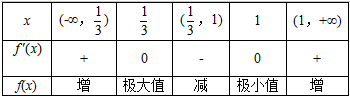
20.设函数f(x)=ax3-(a+b)x2+bx+c,其中a>0,b,c∈R。
(1)若
(2)求证:当0≤x≤1时,|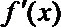
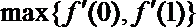
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数


(1)求函数
(2)对于函数


(3)当

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5),
(1)求以向量
(2)若向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某广告公司为2010年上海世博会设计了一种霓虹灯,样式如图中实线分所示。其上部分是以AB为直径的半圆,点O为圆心,下部分是以AB为斜边的等腰直角三角形,DE、DF是两根支杆,其中AB=2 m,∠EOA=∠FOB=2x(0<x<
(1) 试将y表示为x的函数;
(2) 试确定当x取何值时,该霓虹灯整体的“心悦效果”最佳?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(1)若
(2)若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
24.已知函数
(1)若函数


(2)如图,设直线


(3)试比较

正确答案
解析
解析已在路上飞奔,马上就到!