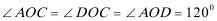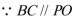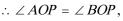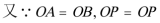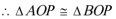- 真题试卷
- 模拟试卷
- 预测试卷
1.已知全集U=R,集合A={x|x<一1或x>4},B={x|-2≤x≤3},那么阴影部分表示的集合为()
正确答案
解析
由韦恩图可知阴影部分表示的集合为
又集合A={x|x<一1或x>4)}={X| 
所以
考查方向
解题思路
1、由韦恩图可知阴影部分表示的集合为
2、集合A={x|x<一1或x>4)}={X| 
易错点
本题易在观察韦恩图时发生错误,易忽视补集的运算。
知识点
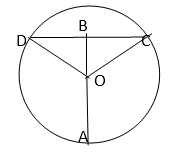
6.哈尔滨文化公同的摩天轮始建于2003年1月15日,2003年4月30日
竣工,是当时中国第一高的巨型摩天轮.其旋转半径50米,最高点距地
面110米,运行一周大约21分钟.某人在最低点的位置坐上摩天轮,则
第14分钟时他距地面大约为()米.
正确答案
解析
如图,
根据周期可知第14分钟时从最低点A处转到了D处,D点距离地面
距离为:AB+10(米)由图知AB=50+25=75(米)
则第14分钟时他距地面大约为85米
故选B
考查方向
解题思路
1、根据题意建立圆模型,利用圆中的知识计算高度。
2、在圆中计算出结果后再加上10米。
易错点
1、本题易在建立圆模型上出错。
2、本题易忽视摩天轮最低点距地面的高度10米。
知识点
8.在平面直角坐标系xOy中,已知△ABC的顶点A(0,3)和C(0,-3),顶点B在椭圆
上,则
正确答案
解析
由题可知
故选A
考查方向
解题思路
1、先根据题意做图,从而发现A点和C点为焦点。
2、在
易错点
1、本题易在理解题意上出现错误。
2、本题易在正弦定理的应用时不能灵活的把椭圆定义与三解形相结合而出错。
知识点
11.已知点O是△ABC外心,AB=4,AO=3,则
正确答案
解析
如图以O为原点,平行于AB的直线为X轴,建立平面直角坐标系,
则A


所以



所以

故选D
考查方向
解题思路
1、由题目中的“O”想到建立坐标系从而把问题转化成向量坐标运算。
易错点
1、本题易在题意理解上出错从而导致无法打开思路。
2、本题不容易想到向量的坐标法而导致无法建立合理的数形结合模型,以及在三角有界性应用上出错。
知识点
2.若复数z满足iz= 2-4i,则z在复平面内对应的点的坐标是()
正确答案
解析
由iz= 2-4i可知
故选C
考查方向
解题思路
先计算Z再找对应点。
易错点
本题易在复数运算上发生错误,易把坐标与复数的实部和虚部关系弄反。
知识点
3.右图所示的程序运行后输出的结果是()
正确答案
解析
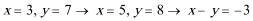
考查方向
解题思路
分条件不断赋值即可
易错点
1、本题易在认识条件语句时出错。
2、本题在赋值时,易在程序先后顺序上出错。
知识点
4.如图所示的数阵中,每行、每列的三个数均成等差数列,如果数阵中所有数之和等于63,那么 a52=()
正确答案
解析
由题可知
得a52=7
故选C
考查方向
解题思路
1、先根据每行等差可知
2、再要根据列等差可知
易错点
1、本题易出现的问题是审题出错。
2、本题易在等距公式的运算上出错。
知识点
5.“吸烟有害健康,吸烟会对身体造成伤害”,哈尔滨市于2012年5月31日规定室内场所禁止
吸烟.美国癌症协会研究表明,开始吸烟年龄(X)分别为16岁、18岁、20岁和22岁,其得
肺癌的相对危险度(Y)依次为15.10、12.81、9.72、3.21;每天吸烟(U)10支、20支、30支者,其
得肺癌的相对危险度(v)分别为7.5、9.5和16.6.用r1表示变量X与y之间的线性相关系数,用
r2表示变量U与V之间的线性相关系数,则下列说法正确的是()
正确答案
解析
开始吸烟年龄(X)分别为16岁、18岁、20岁和22岁与得肺癌的相对危险度(Y)依次为15.10、12.81、9.72、3.21做为横纵坐标绘出散点图可得图像走势由左上到右下,所以r1<0;每天吸烟(U)10支、20支、30支者与得肺癌的相对危险度(v)分别为7.5、9.5和16.6做为横纵坐标绘出散点图可得图像走势由左下到右上,所以r2>0。
故选D
考查方向
解题思路
1、吸烟年龄(X)与得肺癌的相对危险度(Y)可根据散点图进行判断。
2、每天吸烟(U)支数与得肺癌的相对危险度(v)也可根据散点图进行判断。
易错点
1、本题由于不能恰当转化成散点图去思考而出错。
2、本题由于没有理解和记住线性相关系数中的r的性质而出错。
知识点
7.原始社会时期,人们通过在绳子上打结来计算数量,即“结绳计数”.当时有位父亲,为了准确记录孩子的成长天数,在粗细不同的绳子上打结,由细到粗,满七进一,那么孩子已经出生多少天?()
正确答案
解析
由题可知绳子由左往右是由细变粗,建立七进制模型得
故选B
考查方向
解题思路
1、建立七进制模型。
2、要据绳子粗细列式计算。
易错点
1、本题多数学生不能由二进制(十进制)所学知识拓宽到此题而无法完成计算。
2、本题建立七进制模型后未看清绳子粗细而运算出错。
知识点
9.如图是某一几何体的三视图,则该几何体的体积是()
正确答案
解析
先计算出长方体的体积V=1×1×2=2其一半为所求几何体的体积即为1。
故选B
考查方向
解题思路
1、先在长方体中切割出原几何体。
2、进行补形再计算其几何体体积,其一半为几何体的体积。
易错点
1、本题易忽视左视图中的虚线而还原几何体时出错。
2、本题在几何体体积计算上不进行补形而计算出错。
知识点
12.已知函数f(x+2)是偶函数,且当x>2时满足xf '(x)>2f '(x)+f(x)),则()
正确答案
解析
根据题意构造
所以

即就是
又由函数f(x+2)是偶函数可知f(x)关于
所以
故选A
考查方向
解题思路
1、由题函数f(x+2)是偶函数可知f(x)关于
2、根据题意构造


易错点
1、本题不易想到函数f(x+2)是偶函数可知f(x)关于
2、本题不容易理解xf '(x)>2f '(x)+f(x))的意思,得不到函数模型,导致题目无法进行。
知识点
10.已知点(n,an)(n∈N*)在y=ex的图象上,若满足Tn=lna1+lna2+……+lnan>k时n的最小值为5,
则k的取值范围是()
正确答案
解析
由已知求出
n=5时

再结合lna1+lna2+- - -+lnan>k及n的最小值为5可知l0≤k<15
故选C
考查方向
解题思路
1、由已知求出

2、再由求出n=5时

易错点
1、本题易在利用二次函数求最值时不考虑n取整数而出错。
2、本题在对lna1+lna2+- - -+lnan>k式中“>”及“n的最小值为5”的理解上出现偏差而导致K能否取10出错。
知识点
15.若函数y=ex-a(e为自然常数)的图象上存在点(x,y)满足约束条件
正确答案
解析
作可行域如图中阴影部分所示
再平移y=ex-a的图像与区域相交,可知在点(0,0)处
y=ex-a与
在点(5,-1)处得a的最大值为
故实数a的取值范围是
考查方向
解题思路
1、根据不等式组画平面区域,并画出函数y=ex-a的图像。
2、平移y=ex-a的图像与区域相交,从而找出最优解,并代入得到a的范围。
易错点
1、本题易在根据不等式组画平面区域时出错。
2、本题容易忽视“-a” 中的“-”而出错。
知识点
13.二项式(x+
正确答案
28
解析
由题可知


故此题答案为28。
考查方向
解题思路
先写出通项再根据题意找出常数项,即就是
易错点
1、本题易在书写通项时出错 。
2、此类题目要教会学生把通项化归成“
知识点
14.在某次数学考试中,甲、乙、丙三名同学中只有一个人得了优秀.当他们被问到谁得到了优秀时,丙说:“甲没有得优秀”;乙说:“我得了优秀”;甲说:“丙说的是真话”.事实证明:在这三名同学中,只有一人说的是假话,那么得优秀的同学是____.
正确答案
丙
解析
根据“只有一个人得了优秀”和“只有一人说的是假话”假设甲说假话,即就是丙也说假话,这与“只有一人说的是假话” 矛盾;再假设丙说假话即就是甲也说假话,又与“只有一人说的是假话” 矛盾;因此乙说了假话,所以丙优秀。
故此题答案为丙
考查方向
解题思路
本题可用反证法的思想去推理,分别假设甲、乙、丙说真话去找矛盾,再找出正确结果。
易错点
1、本题不易读懂题意,特别是对“只有一个人得了优秀”和“只有一人说的是假话”的理解不到位。
2、本题易出现逻辑上的混乱,从而导致判断出错。
知识点
16.一个棱长为5的正四面体(棱长都相等的三棱锥)纸盒内放一个小正四面体,若小正四面体
在纸盒内可以任意转动,则小正四面体的棱长的最大值为 .
正确答案
解析
因为小正四面体在正四面体纸盒内可以任意转动,所以小正四面体在正四面体纸盒的内切球中,则小正四面体棱长最大时即棱长为球内接正方体的面对角线。设正四面体内切球的半径为R,内切球的内接正方体棱长为

所以小正四面体的棱长的最大值为
故小正四面体的棱长的最大值为
考查方向
解题思路
1、利用等体积计算正四面体内切球半径。
2、计算正四面体内切球内接正方体的棱长,最后算出小正四面体的棱长即可。
易错点
1、本题不易想出如何使小正四面体在纸盒内可以任意转动会转换成什么模型。
2、本题在利用等体积计算正四面体内切球半径和计算球内接正方体的棱长时易出错。
知识点
20. 椭圆C1:

( I )求C1的标准方程;
(Ⅱ)求四边形ABCD的面积的最大值.
正确答案
(1)
解析
试题分析:本题是直线与圆锥曲线综合应用问题,解题时选通过已知条件确定椭圆方程,再根据直线方程计算弦长,最后再求出面积,再利用分式函数最值求法求出最值。
(1)由题意
所以
(2) ①直线



设圆心


整理得
②当直线
当直线
综上,四边形
考查方向
解题思路
本题考查直线与圆锥曲线综合应用问题,解题步骤如下:
1、根据题意求出椭圆方程。
2、设AB、CD直线方程与椭圆联立求出弦AB、CD的长再利用面积公式计算面积。 3、利用分式函数求最值的方法求出最值。
易错点
1、不分直线斜率是否为0而丢分。
2、联立方程和求弦长时容易在运算上出错。
知识点
17. 在△ABC中,角A,B,C的对边分别为a,b,c,已知
(Ⅰ)求
(Ⅱ) 若角A是钝角,且c=3,求b的取值范围.
正确答案
(1)2;(2)
解析
试题分析:本题属于三角形中的正弦定理、余弦定理应用问题,题目的难度适中。(1)求解时一定要定位好是角化边还是边化角;(2)在求边的范围时切记不要忘记三角形中三边关系。
(1)由正弦定理
(2) 由余弦定理


由①②得
考查方向
解题思路
本题考查了正弦定理、余弦定理应用,解题步骤如下:1、分析判断后边化角,利用和角公式整理后再利用角化边。2、由余弦定理解出
易错点
1、第一问边角转化判断失误而错解。2、第二问没想到用三边关系缩小范围而出错。
知识点
18.近两年双11网购受到广大市民的热捧.某网站为了答谢老顾客,在双11当天零点整,每个金冠买家都可以免费抽取200元或者500元代金券一张,中奖率分别是

( I )试求这4人中恰有1人抽到500元代金券的概率;
(Ⅱ ) 这4人中抽到200元、500元代金券的人数分别用X、Y表示,记

正确答案
(1)

解析
试题分析:本题属常见的概率问题,在审题时要从中提炼出概率事件是独立重复实验再下手去做。其难度和其它概率问题一样难度适中,主要是题意的理解。
(1)设“这4人中恰有
(2)易知

考查方向
解题思路
本题考查概率和期望的计算,解题步骤如下:
1、设事件计算概率。
2、找
易错点
1、第一问中在定位成独立重复实验概率问题时易出错。
2、第二问分布列中
知识点
19. 如图,已知多面体4 BCDEF中,ABCD为菱形,∠ABC=60°AE⊥平面ABCD,AE∥CF,AB=AE=1,AF⊥ BE。
( I )求证:平面BAF⊥平面BDE;
(Ⅱ)求二面角B-AF-D的余弦值。
正确答案
(1)略;(2)
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,(1)证明时要找到线面垂直才能下手去做;(2)要注意二面角为钝角这种情况。
(Ⅰ)证明:连


又




又
则


则

所以



所以平面
(Ⅱ)以







求得平面
求得平面
设所求二面角为
则有
又因为所求二面角为钝角
所以所求二面角得余弦值为
考查方向
解题思路
本题考查空间几何体的基本证明和二面角计算,解题步骤如下:
1、利用线面垂直得到一组线线垂直再结合已知证出结论。
2、建系计算出法向量再利用公式得到
易错点
1、第一问不易找准线面垂直关系而没思路。2、第二问判断二面角为钝角上易出错。
知识点
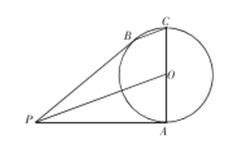
22. 【选修4-1:几何证明选讲】
如图,已知线段AC为⊙O 的直径,P为⊙O的切线,切点为A,B为⊙O上一点,且BC∥PO.
( I )求证:PB为⊙O的切线;
(Ⅱ)若⊙O的半径为1,PA =3,求BC的长。
正确答案
(1)证明略;(2)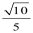
解析
试题分析:本题属于平面几何问题,题目难度较低,解题时要注意深入分析已知条件和特征结论,善于将各已知条件联系起来考虑,寻找合理的解题思路。
(1)连接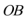
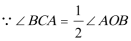
又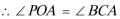
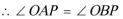
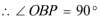
(2)连接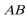
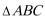
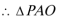
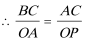
解得
考查方向
解题思路
本题考查三角形与圆的相关知识,解题步骤如下:
1、通过相应的条件和定理建立起有关角或边之间的关系式,如全等关系。
2、灵活三角形相似得到所需结论。
易错点
1、未想到连接OB、AB而无法下手;
2、第二问中由相似得到合适结论出错。
知识点
21. 设函数f(x)=x2一ln(x+a)+b,g(x)=x3.
( I )若函数f(x)在点(0,f(0)))处的切线方程为x+y=0,求实数a,b的值;
(Ⅱ)在(I)的条件下,当X∈(0,+∞)时,求证:f(x)<g(x);
(Ⅲ)证明:对于任意的正整数n,不等式
正确答案
(1)
解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)直接按照切线问题完成第一问题,要注意方程思想的应用;(2)要学会构造函数模型灵活运用导函数这个工具完成函数的比较大小等;(3)涉及不等式证明问题,要灵活运用不等式证明中最长见的比较方法,如作差法,放缩法,分析法等.
(1)
依题意
(2)由(1)可知函数
则
显然,当



又


即

(3)由(2)知
即


所以原不等式得证
考查方向
解题思路
本题考查导数的性质,解题步骤如下:
1、求导,列方程得到
2、构造函数模型利用导函数求出
3、利用第二问结论再结合不等式中的放缩法完成证明。
易错点
1、求导出错,求单调区间出错。
2、第三问在利用第二问放缩时易出错。