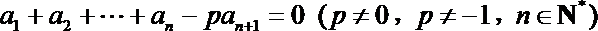- 真题试卷
- 模拟试卷
- 预测试卷
3. 已知函数



正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
1. 已知数集

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 若不等式


正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
6.在平面直角坐标系xOy中,“直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 在△ABC中,若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 根据国家质量监督检验检疫局发布的《车辆驾驶人员血液、呼气酒精含量阈值与检验》(GB19522—2004)中规定车辆驾驶人员血液酒精含量:“饮酒驾车非醉酒驾车”的临界值为20mg/100ml;“醉酒驾车”的临界值为80mg/100ml。某地区交通执法部门统计了5月份的执法记录数据:
根据此数据,可估计该地区5月份“饮酒驾车” 发生的频率等于( )
正确答案
0.09
解析
解析已在路上飞奔,马上就到!
知识点
2. 已知x是实数,
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
9.已知△ABC中,AB边上的高与AB边的长相等,则 
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设正四棱锥的侧棱长为1,则其体积的最大值为( )
正确答案
解析
法1 设正四棱锥的底面边长为






法2 设正四棱锥的侧棱与底面所成角为





知识点
11.已知平面向量









正确答案
解析
设

由



且
知识点
12.在平面直角坐标系xOy中,过点












正确答案
解析
设



令


知识点
14.在平面直角坐标系xOy中,直角三角形ABC的三个顶点都在椭圆



正确答案
3
解析
设AB的方程为:






故
所以
令


由



知识点
13.定义:

正确答案
解析
易得


知识点
7. 如图,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知△ABC内接于单位圆(半径为1个单位长度的圆),且
(1)求角
(2)求△ABC面积的最大值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在平面直角坐标系



(1)过点







(2)已知点









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数




(1)求此平行线间的距离;
(2)若存在


(3)对于函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.如图,在四面体ABCD中,
(1)若EF∥平面ABD,求实数
(2)求证:平面BCD⊥平面AED。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图甲,一个正方体魔方由27个单位(长度为1个单位长度)小立方体组成,把魔方中间的一层



(1)试用

(2)求魔方增加的表面积的最大值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.【选做题】
本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答。若多做,则按作答的前两题评分。解答时应写出文字说明、证明过程或演算步骤。
A.几何证明选讲
如图,已知AP切圆O于点P,AC交圆O于B、C两点,点M是BC的中点。

求证:
B.矩阵与变换
将曲线



C.极坐标与参数方程
在平面直角坐标系xoy中,求直线


D.不等式选讲
已知x,y,z均为正数。求证:
正确答案
A.
B.
C.
D.
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列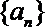
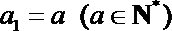
(1)求数列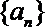
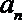
(2)若对每一个正整数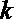
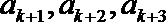
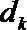
①求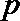
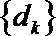
②记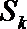
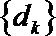
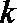
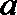
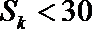

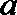
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.考察


一个自然的推广引导我们去猜想下面的命题:
若

试用数学归纳法证明上述命题。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.某养鸡场流行一种传染病,鸡的感染率为10%.现对50只鸡进行抽血化验,以期查出所有病鸡。设计了如下方案:按n(

(1)若n

(2)为了减少化验次数的期望值,试确定n的大小。
正确答案
解析
解析已在路上飞奔,马上就到!