- 真题试卷
- 模拟试卷
- 预测试卷
6.当


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设集合P={-1,0,1},集合Q={0,1,2,3},定义P*Q=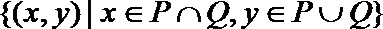
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.一个算法的程序框图如下图所示,若执行该程序输出的结果为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.在平面直角坐标系中,若不等式组
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.如果直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.定义域是一切实数的函数






①

②“
③

其中正确结论的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知平面上三个点A、B、C满足

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设

正确答案
105
解析
解析已在路上飞奔,马上就到!
知识点
12.若不等式|3x-b|<4的解集中的整数有且仅有1,2,3,则b的取值范围___________。
正确答案
(5,7)
解析
解析已在路上飞奔,马上就到!
知识点
15.将正整数1,2,3,4,…,n2(n≥2)任意排成n行n列的数表,对于某一个数表,计算各行和各列中的任意两个数a,b(a>b)的比值

则(1)f(3)=___________;
(2)f(2013)=___________。
正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
10.如图是某几何体的三视图,则该几何体的外接球的体积为___________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设


正确答案
11
解析
解析已在路上飞奔,马上就到!
知识点
13.已知点M是抛物线

正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
9.已知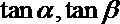
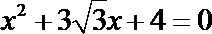
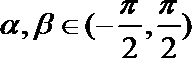
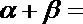
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,在矩形ABCD中,AB=2,BC=
(I)线段BC上存在点Q,使PQ⊥QD,求
(II)线段BC上存在唯一点Q,使PQ⊥QD时,求二面角A-PD-Q的余弦值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知F1、F2是椭圆


(Ⅰ)求椭圆的标准方程;
(Ⅱ)⊙O是以F1F2为直径的圆,一直线l: y=kx+m与⊙O相切,并与椭圆交于不同的两点A、B. 当

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设函数


(1)求数列
(2)证明:对任何正整数

(3)若数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.△ABC中,角A、B、C对边分别是a、b、c,满足
(Ⅰ)求角A的大小;
(Ⅱ)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知等差数列





(1)求数列

(2)设数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.
(1)设AB=x米,cosA=f(x),求f(x)的解析式,并指出x的取值范围;
(2)求四边形ABCD面积的最大值.
正确答案
解析
解析已在路上飞奔,马上就到!