理科数学泉州市2010年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

2．下列函数中，在其定义域内既是奇函数又是减函数的是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二元二次方程表示圆的条件

题型：单选题

分值: 5分

4．函数过定点（）

A（1,2）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

题型：单选题

分值: 5分

5．“”是“直线平行于直线”的（）

A充分而不必要条件

B必要而不充分条件

C充分必要条件

D既不充分也不必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

简单复合函数的导数

题型：单选题

分值: 5分

7．若PQ是圆的弦，PQ的中点是（1,2）则直线PQ的方程是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

9．已知抛物线的焦点为，准线与轴的交点为为抛物线上的一点，且满足，则=（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

分值: 5分

1．设函数定义域为，，则下列关系中正确的是（）

AM=P

BM∪P=P

CM∪P=M

DM∩P=P

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：单选题

分值: 5分

3．一个几何体的三视图如右图，其中主视图和左视图都是边长为2的正三角形，那么这个几何体的表面积为（　　）

D3π

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：单选题

分值: 5分

8．△ABC中，，则△ABC的面积等于（）.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦定理

题型：单选题

分值: 5分

10．定义：平面内两条相交但不垂直的数轴构成的坐标系（两条数轴的原点重合且单位长度相同）称为平面的斜坐标系；在平面的斜坐标系中，若（其中分别是斜坐标系轴、轴正方向上的单位向量，、，为坐标原点），则称有序数对为点的斜坐标。在平面的斜坐标系中，若=，点M的斜坐标为，则以M为圆心，半径为1的圆在斜坐标系中的方程为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面向量数量积的运算直线的一般式方程

题型：单选题

分值: 5分

6．关于直线，及平面α，β，下列命题中正确的是（）

A若l∥α，αβ=m，则l∥m

B若l⊥α，l∥β，则α⊥β

C若∥α，m∥α，则∥m

D若l∥α，m⊥l，则m⊥α

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用空间中直线与直线之间的位置关系空间中直线与平面之间的位置关系平面与平面之间的位置关系

填空题本大题共5小题，每小题4分，共20分。把答案填写在题中横线上。

题型：填空题

分值: 4分

11．若抛物线的焦点与双曲线的右焦点重合，则的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 4分

13．由曲线及坐标轴围成的曲边梯形的面积是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两条直线垂直的判定

题型：填空题

分值: 4分

12．已知，则的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的图像

题型：填空题

分值: 4分

14．已知是的零点，且，则从小到大的顺序是。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 4分

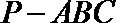
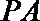
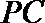
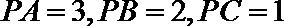
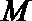
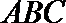
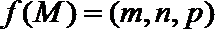
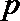
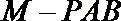
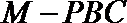
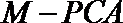
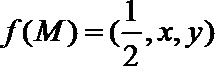
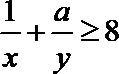
15．如图,在三棱锥中, 、、两两垂直,且.设是底面内一点,定义,其中、、分别是三棱锥、三棱锥、三棱锥的体积.若,且恒成立,则正实数的最小值为________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二元二次方程表示圆的条件

简答题（综合题）本大题共80分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 13分

16．已知函数，．

（I）求的最大值和最小值；

（II）若不等式在上恒成立，求实数的取值范围．

正确答案

（Ⅰ）

．

又，，即，

．

（Ⅱ），，

且，

，即的取值范围是．

解析

解析已在路上飞奔，马上就到！

知识点

幂函数图象及其与指数的关系

题型：简答题

分值: 13分

19．最近北方遭受雪灾，蔬菜告急，南方某蔬菜公司要将一批蔬菜从南方A地运到北方B地，有汽车、火车两种运输工具可供选择，两种运输工具的主要参考数据如下表：

若这批蔬菜在运输过程（含装卸时间）中损耗为300元/h，设A、B 两地距离为km

（I）设采用汽车与火车运输的总费用分别为、，求、的表达式；

（II）试根据A、B两地距离大小比较采用哪种运输工具比较好（即运输总费用最小）．

（注：总费用＝途中费用＋装卸费用＋损耗费用）

正确答案

（Ⅰ）由题意可知，用汽车运输的总支出为：

用火车运输的总支出为：

（Ⅱ）由得；

由得

答：当A、B两地距离小于时，采用汽车运输好

当A、B两地距离等于时，采用汽车或火车都一样

当A、B两地距离大于时，采用火车运输好

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：简答题

分值: 14分

21．已知是函数的极值点。

（1）求实数的值；

（2）若函数恰有一个零点，求实数的范围；

（3）当时，函数的图象在处的切线与轴的交点是。若，问是否存在等差数列，使得对一切都成立？若存在，求出数列的通项公式；若不存在，请说明理由。

正确答案

（1）=

又x=0是的极值点，

（2）由（1）知

当时，，函数恰有一个零点

当时，，当变化时，与变化情况如下：

由上表知函数的极大值为，又

由函数的图象变化知，函数恰有一个零点时，

的取值范围为或

综上所述：当时，

当时，或

（3），，

函数的图象在处的切线为，

又其切线与轴的交点是，代入上述方程整理得 ①

，代入（1）式整理得，

是等比数列，

假设存在等差数列，使得对一切都有

②

当时， ③

②-③得

又，满足

且，即是等差数列

存在等差数列，使得对一切都有

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

分值: 13分

17．将如图1的直角梯形ABEF（图中数字表示对应线段的长度）沿直线CD折成直二面角，连结部分线段后围成一个空间几何体，如图2所示。

（1）求证：；

（2）求二面角D—BF—E的大小；

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：简答题

分值: 14分

20．已知椭圆的中心在坐标原点，焦点在轴上，短轴长为2，且两个焦点和短轴的两个端点恰为一个正方形的顶点。过右焦点与轴不垂直的直线交椭圆于，两点。

（Ⅰ）求椭圆的方程；

（Ⅱ）当直线的斜率为1时，求的面积；

（Ⅲ）在线段上是否存在点,使得以为邻边的平行四边形是菱形？

若存在，求出的取值范围；若不存在，请说明理由。

正确答案

（Ⅰ）由已知，椭圆方程可设为．

∵ 两个焦点和短轴的两个端点恰为正方形的顶点，且短轴长为2，

∴ ．

所求椭圆方程为．

（Ⅱ）右焦点，直线的方程为．

设，

由得，解得．

∴ ．

（Ⅲ）假设在线段上存在点,使得以为邻边的平行四边形是菱形．因为直线与轴不垂直，所以设直线的方程为．

由可得．

∴．

．其中

以为邻边的平行四边形是菱形

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

题型：简答题

分值: 13分

18．已知等差数列{an}中，首项a1＝1，公差d为整数，且满足a1+3＜a3，a2+5＞a4，数列{bn}满足，其前n项和为Sn．

（1）求数列{an}的通项公式an；

（2）若S2为S1，Sm（m∈N*）的等比中项，求正整数m的值．

正确答案

（1）由题意，得解得< d <．

又d∈Z，∴d = 2．∴an=1+(n－1)2=2n－1．

（2）∵，

∴．

∵，，，S2为S1，Sm(m∈)的等比中项，

∴，即，

解得m=12．

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式等差数列的性质及应用等比数列的性质及应用裂项相消法求和

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷